Processus géostatistique

Disponible avec une licence Geostatistical Analyst.

Dans cette rubrique, un processus généralisé des études géostatistiques est présenté et les principales étapes sont expliquées. Comme indiqué dans la rubrique Présentation des géostatistiques, les géostatistiques sont une classe de statistiques qui permettent d’analyser et de prévoir les valeurs associées à des phénomènes spatiaux ou spatiotemporels. Geostatistical Analyst fournit un ensemble d’outils qui permet la construction de modèles utilisant des coordonnées spatiales. Ces modèles peuvent être appliqués à une grande variété de scénarios et sont généralement utilisés pour générer des prévisions pour des localisations non échantillonnées, ainsi que des mesures d’incertitude de ces prévisions.

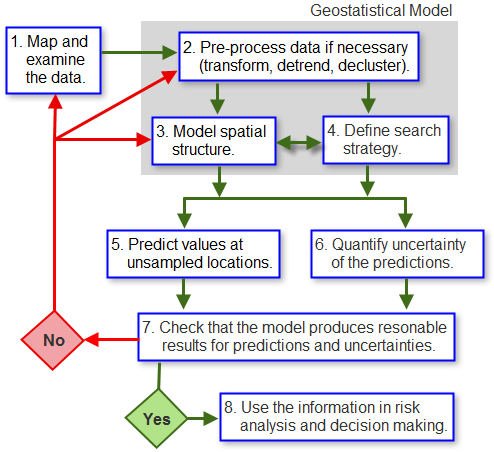
La première étape, comme dans toute étude dynamique, consiste à examiner attentivement les données. Cela commence généralement par la cartographie du jeu de données, avec une classification et une combinaison de couleurs qui permettent de visualiser clairement les caractéristiques importantes présentées par le jeu de données, par exemple, une forte augmentation des valeurs du nord au sud ou un mélange de valeurs élevées et faibles sans disposition particulière (signe éventuel que les données ont été prises à une échelle qui ne montre aucune corrélation spatiale).

La seconde étape consiste à créer le modèle géostatistique. Ce processus peut impliquer plusieurs étapes, en fonction des objectifs de l’étude (à savoir, les types d’informations que le modèle est supposé fournir) et des entités du jeu de données considérées comme suffisamment importantes pour être intégrées. Lors de cette étape, les informations collectées pendant une exploration rigoureuse du jeu de données et avant d’avoir connaissance du phénomène déterminent la complexité du modèle ainsi que la précision des valeurs interpolées et des mesures d’incertitude. Dans la figure ci-dessus, la création du modèle peut impliquer le prétraitement des données pour supprimer les tendances spatiales qui sont modélisées séparément et rajoutées à l’étape finale de l’interpolation. Elle peut également impliquer la transformation des données pour faire en sorte qu’elles suivent davantage une distribution gaussienne (requise par certaines méthodes et sorties de modèle). Alors qu’une grande quantité d’informations peut être obtenue par l’examen du jeu de données, il est important d’intégrer toutes les connaissances que vous pourriez avoir sur le phénomène. Le modélisateur ne peut pas reposer uniquement sur le jeu de données pour afficher toutes les entités importantes ; celles qui n’apparaissent pas peuvent toujours être intégrées dans le modèle par l’ajustement des valeurs de paramètre pour refléter un résultat attendu. Il est important que le modèle soit aussi réaliste que possible pour que les valeurs interpolées et les incertitudes associées représentent avec précision des phénomènes réels.

Outre le prétraitement des données, il peut s’avérer nécessaire de modéliser la structure spatiale (corrélation spatiale) dans le jeu de données. Certaines méthodes, comme le krigeage, exigent qu’elle soit explicitement modélisée avec des fonctions de semi-variogramme ou de covariance (reportez-vous à la rubrique Semi-variogrammes et fonctions de covariance), tandis que d’autres méthodes, comme la pondération par l’inverse de la distance, reposent sur un degré supposé de structure spatiale, que le modélisateur doit fournir en fonction de connaissances préalables sur le phénomène.

La stratégie de recherche est un composant final du modèle. Elle définit dans quelle mesure les points de données sont utilisés pour la génération d’une valeur pour une localisation non échantillonnée. Il est également possible de définir leur configuration spatiale (localisation les uns par rapport aux autres et par rapport à la localisation non échantillonnée). Ces deux facteurs affectent la valeur interpolée et l’incertitude associée. Dans le cas de nombreuses méthodes, une ellipse de recherche est définie, ainsi que le nombre de secteurs qui fractionnent l’ellipse et le nombre de points pris à partir de chaque secteur pour la réalisation d’une prévision (reportez-vous à la rubrique Voisinages de recherche).

Une fois le modèle complètement défini, il peut être utilisé conjointement avec le jeu de données afin de générer des valeurs interpolées pour toutes les localisations non échantillonnées dans une zone d’intérêt. La sortie est généralement une carte qui affiche les valeurs de la variable en cours de modélisation. L’effet des points aberrants peut être examiné à ce stade puisqu’ils modifient probablement les valeurs de paramètre du modèle, et donc la carte interpolée. Selon la méthode d’interpolation, le même modèle peut également être utilisé pour générer des mesures d’incertitude pour les valeurs interpolées. Tous les modèles ne disposant pas de cette fonctionnalité, il est important de définir dès le début si des mesures d’incertitude sont nécessaires. Vous pouvez ainsi identifier les modèles les plus adaptés (reportez-vous à la rubrique Arbres de classification).

Comme dans toute modélisation, il convient de vérifier la sortie du modèle, c’est-à-dire, de vous assurer que les valeurs interpolées et les mesures d’incertitude associées sont raisonnables et correspondent à vos attentes.

Une fois que vous êtes satisfait du modèle créé et ajusté, et que vous avez vérifié sa sortie, vous pouvez utiliser les résultats dans des analyses de risque et lors de prises de décision.