Fonctionnement de l’outil Composantes principales multidimensionnelles

Disponible avec une licence Image Analyst.

L’analyse en composantes principales (ACP) est une technique classique utilisée pour l’analyse exploratoire des données. Elle est souvent utilisée pour réduire la dimensionnalité du jeu de données de sorte que vous puissiez identifier les entités et les modèles des données. Dans une analyse multivariée, l’ACP peut ainsi identifier les variables qui sont nécessaires et celles qui sont exclues sans que cela n’influe sur le résultat de l’analyse. Dans l’analyse des images multispectrales et hyperspectrales, l’outil Composantes principales multidimensionnelles permet de calculer un jeu de composantes principales capturant la plupart des informations et autorisant l’analyse sur un nombre réduit de bandes. Les données de séries chronologiques d’images sont devenues plus courantes, mais posent des problèmes pour identifier et extraire des informations ciblées. Cet outil fait appel à la technique de l’ACP pour analyser les données de série chronologique ou les données raster multidimensionnelles.

Analyse en composantes principales des données raster multidimensionnelles

Un raster multidimensionnel contient une ou plusieurs variables. L’outil Composantes principales multidimensionnelles analyse une variable à la fois, un cube d’image 3D avec des coordonnées (x,y,temps) ou (x,y,z) et transforme le cube d’image 3D en un jeu de composantes principales dans lequel la variance est maximisée de sorte qu’il soit possible d’identifier et d’extraire les entités et les modèles figurant dans les données. Vous pouvez afficher un cube de données d’image de deux façons : avec un jeu d’images (tranches), chacune représentant une image dans le temps ou avec un jeu de tableaux dimensionnels, chacun représentant une série chronologique de pixels (profil temporel). Dans l’exemple suivant, les données d’image de série chronologique servent à décrire la fonctionnalité, sachant que l’outil peut s’appliquer aux données comportant une dimension non temporelle :

Le mode de réduction des dimensions analyse un ensemble d’images.

Le mode Réduction spatiale analyse des pixels dans la série chronologique.

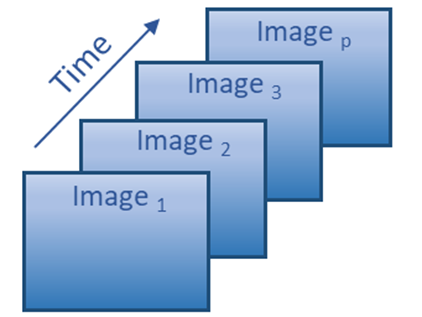
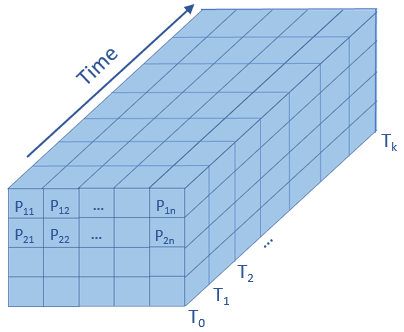
Vous pouvez appliquer une analyse en composantes principales à l’aide du mode de réduction des dimensions et du mode de réduction spatiale. Le traitement via ces deux modes implique deux applications différentes.

• Le mode de réduction des dimensions analyse les données en tant qu’ensemble d’images. Il transforme et réduit les données en un ensemble d’images qui capturent les entités et modèles dominants. Vous pouvez, par exemple, extraire les pixels dominants dans une série chronologique d’images et cartographier les changements affectant le plan d’eau au fil du temps. Le mode de réduction des dimensions est souvent utilisé dans les analyses de séries chronologiques d’images en ce qui concerne les données liées au sol, telles que les séries chronologiques NDVI.
• Le mode de réduction spatiale analyse les données en tant qu’ensemble de pixels dans la série chronologique. Il identifie les principaux modèles temporels ainsi que les localisations spatiales associées des modèles temporels. Par exemple, vous pouvez extraire le modèle temporel interannuel des événements El Niño et La Niña à l’aide des données de température à la surface de la mer et de leurs localisations. Cette option convient pour l’analyse de longues séries chronologiques, mais pas pour des données haute résolution.

Exemple de l’outil Composantes principales multidimensionnelles

Dans l’exemple figurant ci-dessous, la série chronologique d’images contient un nombre k d’images X₁, X₂, …, X_k ; la composante principale calculée est une combinaison linéaire des images exprimée comme suit :

PC1 = a11X1 + a12X2 + … + a1kXk

Sa forme matricielle pour toutes les composantes principales est :

Y = XA

où :

Y = (PC1, PC2, …, PCk)

est la matrice contenant les composantes principales et

X = (X1, X2, …, Xk)

est la matrice contenant les données en entrée.

La matrice A contient les coefficients qui transforment les données d’origine en composantes principales. Les valeurs de la matrice A sont appelées chargements et décrivent dans quelle mesure chaque image contribue à une composante principale en particulier. Un chargement important signifie que l’image noue une relation forte à une composante principale donnée. Le signe d’un chargement indique si l’image et une composante principale sont corrélées positivement ou négativement.

Les colonnes normalisées dans une matrice A sont des vecteurs propres qui spécifient les orientations des composantes principales par rapport aux images d’origine. Les valeurs propres calculées avec les vecteurs propres indiquent les variances expliquées par chaque composante principale. Les valeurs propres, classées de la plus grande à la plus petite, déterminent l’ordre des composantes principales.

La première composante est calculée de sorte qu’elle représente la plus grande variance possible dans les données, la deuxième composante représente la variance la plus élevée suivante, à condition qu’elle ne soit pas corrélée (perpendiculaire) à la première composante, et ainsi de suite. Le calcul se poursuit jusqu’à ce que le nombre total de composantes spécifiées soit atteint. Toutes les informations contenues dans les données d’origine sont préservées si vous calculez toutes les composantes principales.

Pour plus d’informations, reportez-vous à Présentation de l’analyse en composantes principales (ACP).

Consultez l’outil Composantes principales multidimensionnelles pour obtenir plus de détails.