Voisinages de recherche

Disponible avec une licence Geostatistical Analyst.

Par principe, plus les localisations sont éloignées de la localisation de la prévision, plus les valeurs mesurées perdent leur autocorrélation spatiale avec la localisation de la prévision. Puisque ces points n’ont que peu ou pas d’effet sur la valeur prévue, ils peuvent être éliminés du calcul de ce point de prévision particulier par la définition d’un voisinage de recherche. Il est également possible que des localisations distantes puissent avoir une influence néfaste sur la valeur prévue si elles se situent dans une zone qui possèdent des caractéristiques différentes de celles de la localisation de la prévision. Enfin, vous pouvez utiliser les voisinages de recherche pour améliorer la vitesse de calcul. Si vous disposez de 2 000 localisations de données, la matrice est trop grande pour être inversée et il est alors impossible de générer une valeur prévue. Plus le voisinage de recherche est petit, plus la génération des valeurs prévues est rapide. Il est par conséquent courant de limiter le nombre de points utilisés dans une prévision en spécifiant un voisinage de recherche.

La forme spécifiée du voisinage restreint l’éloignement et la localisation de recherche des valeurs mesurées à utiliser dans la prévision. D’autres paramètres restreignent les localisations qui sont utilisées dans le voisinage de recherche. Il est possible de modifier le voisinage de recherche en modifiant sa taille et sa forme ou en modifiant le nombre de voisins qu’il comporte.

La forme du voisinage est influencée par les données en entrée et la surface que vous essayez de créer. Si l’autocorrélation spatiale des données ne comporte aucune influence directionnelle (pour plus d’informations, reportez-vous à la rubrique Prise en compte des influences directionnelles), vous pouvez utiliser les points de manière égale dans toutes les directions ; la forme du voisinage de recherche est alors un cercle. Toutefois, si les données comportent une tendance ou une autocorrélation directionnelle, vous pouvez orienter la forme du voisinage vers une ellipse dont le grand axe est parallèle à la direction de l’auto-corrélation à long terme (direction dans laquelle les données sont le plus similaires).

Le voisinage de recherche peut être spécifié dans Geostatistical Wizard (Assistant géostatistique), comme indiqué dans l’exemple suivant :

• Type de voisinage : Standard
• Nombre maximal de voisins = 4
• Nombre minimal de voisins = 2
• Type de secteur (stratégie de recherche) : quatre secteurs avec un décalage de 45° ; rayon = 182955,6

Étape du voisinage de recherche

Les pondérations utilisées pour estimer la valeur à la localisation signalée par le réticule sur la surface d’aperçu sont indiquées dans l’image ci-dessus. Les points de données avec les pondérations les plus élevées sont mis en évidence en rouge.

Une fois la forme du voisinage spécifié, vous pouvez limiter les localisations à utiliser au sein de cette forme. Vous pouvez définir les nombres maximal et minimal de voisins à inclure et diviser le voisinage en secteurs pour vous assurer que les valeurs de toutes les directions soient incluses. Si vous divisez le voisinage en secteurs, les nombres maximal et minimal de voisins sont appliqués à chaque secteur.

Vous pouvez utiliser différents types de secteurs :

• Un secteur
• Ellipse avec quatre secteurs
• Ellipse avec quatre secteurs et un décalage de 45 degrés
• Huit secteurs

Le krigeage utilise la configuration de données spécifiée par le voisinage de recherche conjointement avec le modèle de semi-variogramme ajusté ; il est possible de déterminer des pondérations pour les localisations mesurées. À l’aide des pondérations et des valeurs mesurées, il est possible de calculer une prévision pour la localisation de la prévision. Ce processus est exécuté pour chaque localisation dans la zone d’étude, de manière à créer une surface continue. D’autres méthodes d’interpolation suivent le même processus, mais les pondérations sont déterminées avec des techniques qui n’impliquent pas de modèle de semi-variogramme.

Le nombre maximal de voisins pouvant être utilisés dépend de la méthode d’interpolation. Pour un seul secteur, le nombre maximal de voisins pour chaque méthode est le suivant :

• Interpolation surfacique : 200 voisins
• Interpolation par diffusion avec interruptions : aucune limite du nombre de voisins
• Krigeage bayésien empirique : 64 voisins
• Prévision de la régression EBK : 64 voisins
• Interpolation polynomiale globale : n’utilise pas de voisinage de recherche
• Pondération par l’inverse de la distance : 1 000 voisins
• Interpolation par noyaux avec interruptions : aucune limite du nombre de voisins
• Krigeage (autre que le krigeage bayésien empirique) : 200 voisins
• Interpolation polynomiale locale : 1 000 voisins
• Fonctions de base radiale : 64 voisins

Le nombre maximal de voisins est affecté lorsque des nombres différents de secteurs sont utilisés ; par exemple, lorsque quatre secteurs sont employés, divisez le nombre de voisins par quatre, et pour huit secteurs, divisez le nombre par huit.

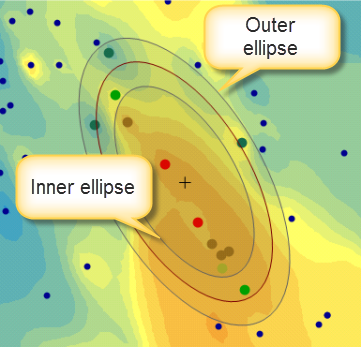
L’option d’interpolation lisse crée trois ellipses. L’ellipse centrale utilise les valeurs Major semiaxis (Demi-grand axe) et Minor semiaxis (Demi-petit axe). L’ellipse intérieure utilise ces valeurs de demi-petit axe et de demi-grand axe multipliées par 1 moins la valeur de Smoothing factor (Facteur de lissage), alors que l’ellipse extérieure utilise ces valeurs de demi-petit axe et de demi-grand axe multipliées par 1 plus le facteur de lissage. Tous les points de ces trois ellipses sont utilisés dans l’interpolation. Des pondérations sont affectées aux points situés dans l’ellipse la plus petite, de la même manière que vous l’interpolation standard (par exemple, si la méthode employée est l’interpolation pondérée par l’inverse de la distance, les points de l’ellipse intérieure sont pondérés en fonction de leur distance de la localisation de la prévision). Des pondérations sont affectées aux points situés entre l’ellipse intérieure et l’ellipse extérieure de la même manière que pour les points situés dans l’ellipse intérieure, mais les pondérations sont ensuite multipliées par une valeur sigmoïdale qui diminue à partir de 1 (pour les points situés juste en dehors de l’ellipse intérieure) jusqu’à 0 (pour les points situés juste en dehors de l’ellipse extérieure). Les points de données en dehors de l’ellipse extérieure ont une pondération égale à zéro dans l’interpolation. Voici un exemple :

Surface d’aperçu affichant les pondérations des points de données

Les exceptions suivantes s’appliquent aux descriptions ci-dessus :

• L’interpolation surfacique, qui ne prend en charge qu’un seul secteur.
• Le krigeage bayésien empirique et la prévision de la régression EBK, qui requièrent un voisinage de recherche circulaire ; les paramètres Major semiaxis (Demi-grand axe) et Minor semiaxis (Demi-petit axe) ont donc été remplacés par le paramètre Radius (Rayon). La valeur du rayon représente la longueur du rayon du cercle de recherche.
• Le krigeage bayésien empirique 3D, qui requiert un voisinage de recherche 3D et prend en charge 1, 4, 6, 8, 12 et 20 secteurs.

Dans Geostatistical Analyst, les pondérations de tous les modèles autres que le krigeage sont définis par des fonctions analytiques a priori qui reposent sur la distance à partir de la localisation de la prévision. La plupart des modèles de krigeage prévoient une valeur en utilisant la somme pondérée des valeurs des localisations à proximité. Le krigeage utilise le semi-variogramme pour définir les pondérations qui déterminent la contribution de chaque point de données à la prévision de nouvelles valeurs à des localisations non échantillonnées C’est pourquoi, le voisinage de recherche par défaut employé dans le krigeage est construit avec les portées majeure et mineure du modèle de semi-variogramme.

Une surface continue doit être constituée de données continues, comme des observations de températures. Toutefois, tous les interpolateurs avec un voisinage de recherche local génèrent des prévisions (et des erreurs standard de prévision) qui peuvent être très différentes pour les localisations à proximité si les voisinages sont différents. Pour voir une représentation graphique expliquant ce comportement, reportez-vous à la rubrique Interpolation lisse.

Remarque :

Un modèle qui utilise l’option d’interpolation lisse ne peut pas prévoir de valeurs si le voisinage de recherche ne contient aucun point de données ; certaines zones de la carte sont ainsi susceptibles de rester vierges.