Comprendre l’erreur de mesure

Disponible avec une licence Geostatistical Analyst.

Trois méthodes de krigeage (ordinaire, simple et universel) utilisent des modèles d’erreur de mesure. L’erreur de mesure survient lorsqu’il est possible d’avoir plusieurs observations différentes à la même localisation. Par exemple, si vous souhaitez extraire un échantillon du sol ou de l’air et diviser cet échantillon en plusieurs sous-échantillons à mesurer. Vous pouvez procéder de la sorte si l’instrument qui mesure les échantillons est sujet à quelques variations. Un autre cas peut concerner l’envoi de des sous-échantillons d’un échantillon de sol à différents laboratoires pour analyse. Ou encore, si la variation de la précision de l’instrument est documentée. Dans ce cas, vous pouvez saisir la variation des mesures connue dans le modèle.

Modèle d’erreur de mesure

Le modèle d’erreur de mesure est

Z(s) = µ(s) + ε(s) + δ(s),

où δ(s) est l’erreur de mesure, et µ(s) et ε(s) sont la variation moyenne et la variation aléatoire. Dans ce modèle, l’effet de pépite est composé de la variance de ε(s) (appelée variation à une micro-échelle) et de la variance de δ(s) (appelée erreur de mesure). Dans Geostatistical Analyst, vous pouvez spécifier une proportion de l’effet de pépite estimé en tant que variation à une micro-échelle et variation de mesure, faire en sorte que Geostatistical Analyst estime l’erreur de mesure pour vous si vous avez plusieurs mesures par localisation ou saisir une valeur pour la variation de mesure. En l’absence d’erreur de mesure, le krigeage est un interpolateur exact, ce qui signifie que si vous effectuez une prévision à une localisation où des données ont été collectées, la valeur prévue est la même que la valeur mesurée. Toutefois, en présence d’erreurs de mesure, vous pouvez prévoir la valeur filtrée, µ(s₀) +ε(s₀), qui n’a pas de terme d’erreur de mesure. Aux localisations où des données ont été collectées, la valeur filtrée n’est pas la même que la valeur mesurée.

Dans les versions précédentes d’ArcGIS, la variation de mesure par défaut était de 0 % ; le krigeage était donc un interpolateur exact par défaut. Dans ArcGIS 10, la variation de mesure par défaut est définie sur 100 %, donc les prévisions par défaut aux localisations mesurées sont basées sur la corrélation spatiale des données et des valeurs mesurées aux localisations à proximité. Une erreur de mesure peut être introduite par de nombreuses sources, y compris l’incertitude de l’appareil de mesure, la localisation et l’intégration des données. En pratique, les données parfaitement précises sont extrêmement rares.

Effet du modèle

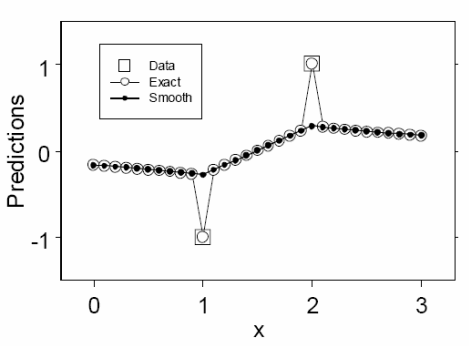
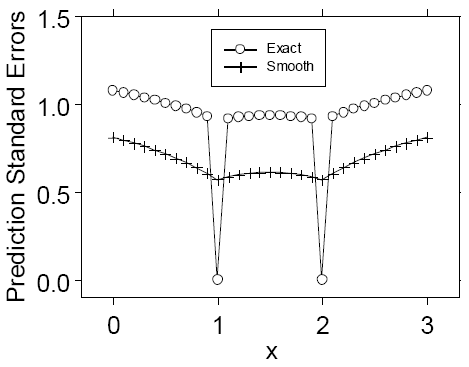
Les modèles d’erreur de mesure permettent d’obtenir une carte finale plus lisse dont les erreurs standard sont inférieures à celle de la version obtenue par le krigeage exact. Ce comportement est illustré par l’exemple des figures ci-dessous, où le krigeage et le krigeage lisse sont représentés lorsqu’il n’existe que deux localisations de données (à 1 et 2) avec des valeurs -1 et 1 pour un modèle sans variation de mesure et un modèle ou l’effet de pépite est uniquement dû à la variation de mesure.