Disponible avec une licence Geostatistical Analyst.
L’interpolation pondérée par l’inverse de la distance (IDW) part de l’hypothèse explicite selon laquelle les objets qui sont proches les unes des autres se ressemblent davantage que ceux qui sont plus éloignés. Pour prévoir la valeur d’une localisation non mesurée, IDW utilise les valeurs mesurées autour de la localisation de prévision. Les valeurs mesurées les plus proches de la localisation de prévision ont plus d’influence sur la valeur prévue que les plus éloignées. IDW suppose que chaque point mesuré possède une influence locale qui diminue avec la distance. Cette interpolation attribue des pondérations plus élevées aux points les plus proches de la localisation de prévision. Les pondérations diminuent en fonction de la distance, d’où le nom de pondération par l’inverse de la distance. Les pondérations attribuées aux points de données sont illustrées dans l’exemple suivant :
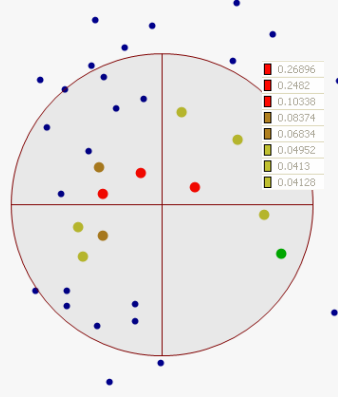
La fenêtre Pondérations contient la liste des pondérations attribuées à chaque point de données qui permet de générer une valeur prévue à la localisation signalée par le réticule.
En savoir plus sur les techniques d’interpolation disponibles dans ArcGIS Geostatistical Analyst
La fonction Puissance
Comme indiqué ci-dessus, les pondérations sont proportionnelles à l’inverse de la distance (entre le point de données et la localisation de prévision) élevée à la valeur de puissance p. Par conséquent, lorsque la distance augmente, les pondérations diminuent rapidement. La vitesse à laquelle les pondérations diminuent dépend de la valeur de p. Si p = 0, aucune réduction n’est liée à la distance, et comme chaque pondération λi est la même, la prévision sera la moyenne de toutes les valeurs de données dans le voisinage de recherche. À mesure que p augmente, les pondérations des points distants diminuent rapidement. Si la valeur p est très élevée, seuls les points situés dans le voisinage immédiat aura une influence sur la prévision.
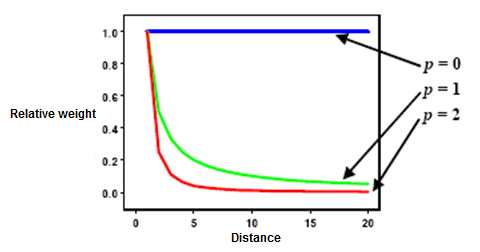
Geostatistical Analyst utilise des valeurs de puissance supérieures ou égales à 1. Lorsque p = 2, la méthode est connue sous le nom d’interpolation au carré pondérée par l’inverse de la distance. La valeur par défaut est p = 2, même s’il n’y a aucune justification théorique à préférer cette valeur plutôt que d’autres. Si vous modifiez p, vous devez en examiner les conséquences dans l’aperçu de la sortie et en étudiant les statistiques de validation croisée.
Le voisinage de recherche
Comme les éléments proches les uns des autres se ressemblent davantage que les plus éloignés, lorsque les localisations s’éloignent, les valeurs mesurées auront peu de relation avec la valeur de la localisation de la prévision. Pour accélérer les calculs, vous pouvez exclure les points les plus distants qui auront peu d’influence sur la prévision. Il est par conséquent courant de limiter le nombre de valeurs mesurées en spécifiant un voisinage de recherche. La forme du voisinage restreint l’éloignement et le lieu de recherche des valeurs mesurées à utiliser dans la prévision. D’autres paramètres de voisinage restreignent les localisations qui seront utilisées dans cette forme. Dans l’image suivante, cinq points mesurés (voisins) seront utilisés pour prévoir la valeur de la localisation sans mesure, le point jaune.
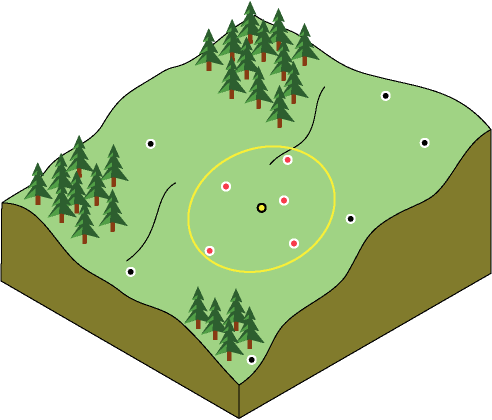
La forme du voisinage est influencée par les données en entrée et la surface que vous essayez de créer. Si vos données ne comportent aucune influence directionnelle, vous pouvez considérer les points comme égaux dans toutes les directions. Pour ce faire, vous allez définir le voisinage de recherche comme un cercle. Cependant, si vos données comporte une influence directionnelle (un vent dominant par exemple), vous pouvez réaliser un ajustement en modifiant la forme du voisinage de recherche en ellipse avec un grand axe parallèle au vent. La prise en compte de cette influence directionnelle est justifiée, car vous savez que les localisations face au vent par rapport à une localisation de prévision vont se ressembler davantage à des distances éloignées que les localisations qui sont perpendiculaires au vent, mais situées plus proches de la localisation de la prévision.
Une fois la forme de voisinage spécifiée, vous pouvez limiter les localisations de données à utiliser dans la forme. Vous pouvez définir le nombre maximal et minimal de localisations à utiliser et diviser le voisinage en secteurs. Si vous divisez le voisinage en secteurs, les contraintes maximales et minimales seront appliquées à chaque secteur.
Les points mis en évidence dans la visualisation de données montrent les localisations et les pondérations qui seront utilisées pour prévoir une localisation au centre de l’ellipse (la localisation du réticule). Le voisinage de recherche est limité à l’intérieur de l’ellipse. Dans l’exemple ci-dessous, les deux points rouges recevront des pondérations supérieures à 10 pour cent. Dans le secteur est, un point (marron) recevra une pondération comprise entre 5 et 10 pour cent. Le reste des points dans le voisinage de recherche recevront des pondérations inférieures.
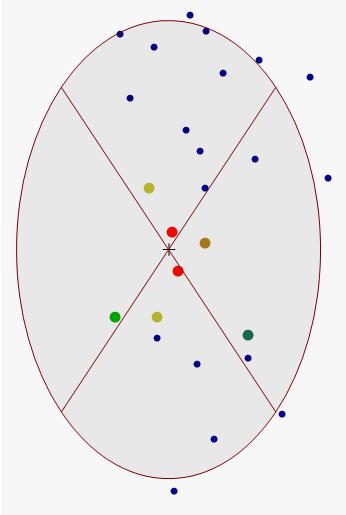
Quand utiliser IDW
Une surface calculée avec IDW dépend de la sélection de la valeur de puissance (p) et de la stratégie du voisinage de recherche. IDW est un interpolateur exact, où les valeurs maximales et minimales (voir le diagramme ci-dessous) dans la surface interpolée peuvent uniquement se produire aux points d’échantillonnage.

La surface en sortie est sensible à l’agrégation et à la présence de points aberrants. IDW suppose que le phénomène qui est modélisé est régi par une variation locale, qui peut être capturée (modélisée) en définissant un voisinage de recherche approprié. Comme IDW ne fournit pas d’erreurs standard de prévision, l’utilisation de ce modèle peut être problématique à justifier.
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?