| Étiquette | Explication | Type de données |
Entités en entrée | Points en entrée représentant les emplacements des points à interpoler. | Feature Layer |
Champ de valeurs | Champ contenant les valeurs à interpoler. | Field |
Table de validation croisée en sortie | Table en sortie contenant les statistiques de validation croisée et les classements de chaque résultat d'interpolation. Les classements finaux des résultats d'interpolation sont stockés dans le champ RANK. | Table |
Couche géostatistique en sortie de classement le plus élevé (Facultatif) | Couche géostatistique en sortie du résultat d'interpolation de classement le plus élevé. Ce résultat d'interpolation possède la valeur 1 dans le champ RANK de la table de validation croisée en sortie. En cas d'égalités pour le résultat d'interpolation de classement le plus élevé ou si tous les résultats sont exclus par les critères d'exclusion, la couche n'est pas créée, même si une valeur est fournie. Des messages d'avertissement sont renvoyés par l'outil si cela se produit. | Geostatistical Layer |
Méthodes d’interpolation (Facultatif) | Spécifie les méthodes d’interpolation qui seront utilisées sur les entités en entrée et un champ de valeur. Pour chaque méthode spécifiée, 1 à 5 résultats d’interpolation sont générés. Par défaut, toutes les méthodes sont générées, à l’exception de la pondération par l’inverse de la distance, des fonctions de base radiale et de l’interpolation polynomiale globale (ces méthodes ne pouvant pas créer d’erreurs standard de prévision). Par défaut, 11 résultats d’interpolation sont générés. Si toutes les options sont spécifiées, 20 résultats d’interpolation sont générés.
| String |
Méthode de comparaison (Facultatif) | Spécifie la méthode à utiliser pour comparer et classer les résultats d'interpolation.
| String |
Critères (Facultatif) | Spécifie le critère à utiliser pour classer les résultats d'interpolation.
| String |
Hiérarchie des critères (Facultatif) | Hiérarchie des critères utilisée pour le tri hiérarchique avec tolérances. Spécifiez plusieurs critères suivant leur ordre de priorité, le premier étant le plus important. Les résultats d'interpolation sont classés en fonction du premier critère et les égalités sont départagées en fonction du deuxième critère. Les égalités dans le deuxième critère sont départagées en fonction du troisième critère et ainsi de suite. Les statistiques de validation croisée étant des valeurs continues qui ne contiennent généralement pas d'égalités exactes, des tolérances sont utilisées pour induire des égalités dans les critères. Pour chaque ligne, spécifiez un critère dans la première colonne, un type de tolérance (en pourcentage ou valeur absolue) dans la deuxième colonne et une valeur de tolérance dans la troisième colonne. Si aucune valeur de tolérance n'est fournie, aucune tolérance n'est utilisée ; cela est particulièrement utile pour la dernière ligne afin d'éviter les égalités pour le résultat d'interpolation de classement le plus élevé. Pour chaque ligne (niveau de la hiérarchie), les critères suivants sont disponibles :
Par exemple, vous pouvez spécifier une valeur Erreur quadratique moyenne (précision) avec une tolérance de 5 % sur la première ligne et une valeur Erreur moyenne (bias) sans tolérance sur la deuxième ligne. Ces options classent d'abord les résultats d'interpolation en fonction de l'erreur quadratique moyenne la plus faible (précision de prévision la plus élevée) et tous les résultats d'interpolation dont les valeurs d'erreur quadratique moyenne diffèrent de moins de 5 % du résultat le plus précis sont considérés comme égaux par la précision de prévision. Parmi les résultats égaux, celui qui possède l'erreur moyenne la plus proche de zéro (bias le plus faible) reçoit le classement le plus élevé. | Value Table |
Critères pondérés (Facultatif) | Plusieurs critères avec pondérations à utiliser pour classer les résultats d'interpolation. Pour chaque ligne, spécifiez un critère et une pondération. Les résultats d'interpolation sont classés indépendamment en fonction de chacun des critères et une moyenne pondérée des classements est utilisée pour déterminer les classements finaux des résultats d'interpolation.
| Value Table |
Critères d'exclusion (Facultatif) | Critères et valeurs associées à utiliser pour exclure de la comparaison des résultats d'interpolation. Les résultats exclus ne sont pas classés et possèdent la valeur No dans le champ Included de la table de validation croisée en sortie.
| Value Table |
Synthèse
Permet de générer différents résultats d’interpolation à partir d’entités ponctuelles en entrée et d’un champ. Les résultats d’interpolation sont ensuite comparés et classés à l’aide de critères personnalisables reposant sur des statistiques de validation croisée.
Les résultats d'interpolation peuvent être classés en fonction d'un seul critère (tel que la précision de prévision la plus élevée ou le bias le plus faible), des classements moyens pondérés de plusieurs critères ou du tri hiérarchique de plusieurs critères (dans lesquels, les égalités pour chacun des critères sont départagées en fonction des critères suivants de la hiérarchie). Des critères d'exclusion peuvent également être utilisés pour exclure de la comparaison des résultats d'interpolation qui ne respectent pas les normes de qualité minimum. La sortie est une table qui récapitule les statistiques de validation croisée et les classements pour chaque résultat d'interpolation. Vous pouvez éventuellement générer une couche géostatistique du résultat d'interpolation de classement le plus élevé à utiliser dans les processus suivants.
Illustration
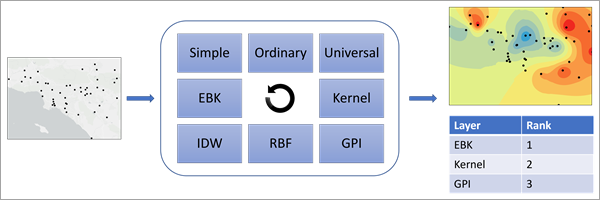
Utilisation
La validation croisée est une méthode de type "leave-one-out" (laisser un élément de côté) qui permet d'évaluer les résultats d'interpolation. Cette méthode supprime chaque point du jeu de données de manière séquentielle et utilise tous les points restants pour prévoir la valeur du point exclu. La prévision par validation croisée est ensuite comparée à la valeur réelle du point masqué et l'écart entre les deux valeurs correspond à l'erreur de validation croisée (cette erreur peut être positive ou négative). En effet, dans la validation croisée, si le résultat d'interpolation permet de prévoir les valeurs des points masqués de manière efficace, il doit également pouvoir permettre de prévoir les valeurs inconnues aux nouvelles localisations, ce qui est l'objectif de l'interpolation. Tous les critères utilisés par cet outil reposent sur les résumés statistiques des résultats de la validation croisée.
L'évaluation des résultats d'interpolation à l'aide des résumés statistiques de la validation croisée représente un moyen pratique et efficace de comparer plusieurs résultats d'interpolation, mais elle ne remplace pas l'expertise des données et l'examen interactif des résultats. L'examen des graphiques et des erreurs de validation croisée individuelles révèle souvent des tendances dans les résultats, qui ne sont pas flagrantes dans les résumés statistiques. Par exemple, il existe souvent des tendances spatiales dans les erreurs de validation croisée où certaines zones sont sous-estimées, tandis que d'autres sont surestimées ; de telles tendances risquent de ne pas être représentées par les résumés statistiques.
En savoir plus sur l'utilisation de la validation croisée pour évaluer les résultats d'interpolation
Le paramètre Méthode de comparaison dispose de trois options permettant de comparer les statistiques de validation croisée des résultats d'interpolation. Chaque option présente des avantages et des inconvénients :
- Critère unique : un critère unique est utilisé pour comparer et classer les résultats. Vous pouvez classer les résultats en fonction de la précision de prévision la plus élevée, du bias le plus faible, de la pire erreur la plus faible, de la précision d'erreur standard la plus élevée ou de la précision la plus élevée. Le critère est fourni dans le paramètre Critère.
- Avantages : cette option représente une méthode simple et courante de comparer les résultats d'interpolation connus pour être stables et réguliers. Elle s'avère également utile pour choisir entre des résultats très similaires.
- Inconvénients : les résultats d'interpolation sont souvent précis pour certains critères, mais pas pour d'autres (par exemple, en ayant une précision de prévision élevée, mais également un bias important). Dans ce cas, le classement en fonction d'un seul critère affecte des classements élevés aux résultats instables ou fallacieux. Lors du classement en fonction d'un seul critère, il est recommandé d'utiliser diverses options du paramètre Critères d'exclusion pour vous assurer que les résultats instables ou fallacieux sont supprimés avant la comparaison.
- Tri hiérarchique avec tolérances : le tri hiérarchique est utilisé pour comparer et classer les résultats. Plusieurs critères sont spécifiés suivant leur ordre de priorité (prioriété la plus élevée en premier) dans le paramètre Hiérarchie des critères. Les résultats d'interpolation sont classés en fonction du premier critère et les égalités sont départagées en fonction du deuxième critère. Les égalités dans le deuxième critère sont départagées en fonction du troisième critère et ainsi de suite. Ce processus est modélisé à partir du Tri personnalisé et du tri hiérarchique dans le tableur (trier en fonction de A, puis de B, puis de C et ainsi de suite). Toutefois, les statistiques de validation croisée étant des valeurs continues qui ne contiennent généralement pas d'égalités exactes, des tolérances (en pourcentage ou valeur absolue) peuvent être spécifiées pour créer des égalités dans chacun des critères.
- Avantages : cette option utilise plusieurs critères et prend en compte les écarts relatifs des statistiques de validation croisée. Par exemple, si un résultat d'interpolation est bien meilleur que le reste selon le critère de priorité la plus élevée, ce résultat d'interpolation reçoit le classement le plus élevé, quels que soient les critères suivants dans la hiérarchie.
- Inconvénients : l'efficacité du tri hiérarchique dépend des valeurs de tolérance fournies. Si les tolérances sont trop faibles, certains critères risquent de ne pas être utilisés car il n'y a aucune égalité à départager. Si les tolérances sont trop importantes, les classements peuvent comporter un grand nombre d'égalités car un grand nombre de résultats sont compris dans les tolérances d'autres résultats.
- Classement moyen pondéré : le classement moyen pondéré de plusieurs critères est utilisé pour comparer et classer les résultats. Plusieurs critères et pondérations associées sont spécifiés dans le paramètre Critères pondérés. Les résultats d'interpolation sont classés indépendamment en fonction de chacun des critères et une moyenne pondérée des classements est utilisée pour déterminer les classements finaux. Les critères dont les pondérations sont les plus grandes ayant davantage d'influence sur les classements finaux, il est possible de les utiliser pour indiquer des préférences pour certains critères par rapport à d'autres.
- Avantages : cette option utilise plusieurs critères, permet de préférer certains critères par rapport à d'autres et utilise toujours l'intégralité des critères dans la comparaison.
- Inconvénients : les écarts relatifs entre les valeurs des statistiques de validation croisée sont ignorés. Par exemple, toutes les erreurs quadratiques moyennes peuvent être comprises à l'intérieur d'une tolérance très faible (ce qui indique que tous les résultats possèdent une précision de prévision similaire), mais elles seront tout de même classées de 1 à N en fonction de la précision de prévision (pour N résultats d'interpolation). Toutefois, les valeurs des erreurs moyennes peuvent varier considérablement entre les résultats (ce qui indique que les bias des résultats sont très différents), mais elles seront tout de même classées de 1 à N en fonction du critère de bias. La moyenne pondérée n'utilisant que les classements des critères, les écarts relatifs dans les statistiques de validation croisée sont ignorés dans le classement.
- Critère unique : un critère unique est utilisé pour comparer et classer les résultats. Vous pouvez classer les résultats en fonction de la précision de prévision la plus élevée, du bias le plus faible, de la pire erreur la plus faible, de la précision d'erreur standard la plus élevée ou de la précision la plus élevée. Le critère est fourni dans le paramètre Critère.
La sortie est une table qui récapitule les statistiques de validation croisée, les descriptions des résultats d’interpolation et les classements. Elle peut être incluse dans une présentation ou un rapport. Les statistiques de validation croisée sont uniquement incluses dans la table si elles s’appliquent à au moins un résultat d’interpolation. Par exemple, si seules la pondération par l’inverse de la distance et les fonctions de base radiale sont utilisées, la table en sortie ne contient pas de champ de valeurs d’erreur standard moyenne, car ces méthodes ne calculent pas les erreurs standard. Si une statistique s’applique à certains résultats d’interpolation, mais pas à d’autres, la valeur sera nulle pour les résultats auxquels la statistique ne s’applique pas. De plus, si Krigeage bayésien empirique a été choisi pour le paramètres Méthodes d’interpolation, plusieurs statistiques de validation croisée seront incluses dans la table alors qu’elles ne sont pas utilisées par les critères de cet outil. Elles sont incluses à titre informatif et leur valeur sera nulle pour toutes les autres méthodes d’interpolation. Si le classement moyen pondéré est utilisé, les classements de tous les critères et leur moyenne pondérée seront également inclus dans la table.
Vous pouvez éventuellement utiliser le paramètre Couche géostatistique en sortie de classement le plus élevé pour créer une couche géostatistique du résultat d’interpolation avec le classement le plus élevé. Cela permet de cartographier le meilleur résultat d’interpolation et de l’utiliser dans d’autres workflows.
Pendant l'exécution de l'outil, les messages de géotraitement et les messages de la barre de progression affichent le résultat d'interpolation en cours de calcul. Une fois que tous les résultats ont été calculés et comparés, les classements sont imprimés commes messages de géotraitement. Les classements sont également disponibles dans la table de validation croisée en sortie.
L’outil Comparer des couches géostatistiques procède aux mêmes comparaisons de validation croisée que cet outil, mais il le fait sur des résultats d’interpolation préalablement créés (couches géostatistiques).
Le tableau ci-après répertorie les critères disponibles, les statistiques de validation croisée qui les mesurent et les formules utilisées pour affecter un score à chaque résultat d'interpolation (les scores plus petits sont préférables). Les classements des critères sont déterminés en triant les scores de chaque résultat d'interpolation.
Remarque :
Pour trois des critères, le score est égal à la statistique de validation croisée.
Critère Statistique de validation croisée Formule des scores Précision de prévision la plus élevée
Erreur quadratique moyenne
Les résultats sont classés en fonction de l'erreur quadratique moyenne la plus petite.
Score = RootMeanSquareError
Bias le plus faible
Erreur moyenne
Les résultats sont classés en fonction de l'erreur moyenne la plus proche de zéro.
Score = AbsoluteValue( MeanError )
Pire erreur la plus faible
Erreur absolue maximum
Les résultats sont classés en fonction de l'erreur absolue maximum la plus petite.
Score = MaximumAbsoluteError
Précision d'erreur standard la plus élevée
Erreur quadratique moyenne standardisée
Les résultats sont classés en fonction de l'erreur quadratique moyenne standardisée la plus proche de la valeur 1.
Score = AbsoluteValue( RMSStdError - 1 )
Précision la plus élevée
Erreur standard moyenne
Les résultats sont classés en fonction de l'erreur standard moyenne la plus petite.
Score = AverageStandardError
En cas d'égalités pour des critères, tous les résultats égaux reçoivent le même classement, égal au classement le plus élevé parmi les classements qu'ils se partagent (où un classement plus élevé représente un numéro de classement plus faible). Par exemple, de la valeur la meilleure à la pire, les valeurs d'erreur quadratique moyenne standardisée (12, 14, 14, 15, 16, 16, 18) reçoivent les classements (1, 2, 2, 4, 5, 5, 7) selon le critère de précision de prévision. Les classements 3 et 6 sont ignorés car leurs valeurs sont égales.
Des égalités peuvent apparaître à diverses phases des comparaisons. Les égalités sont plus courantes lorsque le tri hiérarchique est utilisé car tous les résultats à l'intérieur de la tolérance sont considérés comme égaux et tous les résultats en dehors de la tolérance le sont également. Les égalités sont également courantes dans le classement moyen pondéré si les classements des résultats d'interpolation varient en fonction des différents critères, ce qui peut générer des moyennes pondérées égales pour les classements. Bien que cela ne soit pas courant, des égalités peuvent également se produire dans les comparaisons en fonction d'un seul critère (par exemple, si tous les points possèdent une valeur constante). Les égalités sur un seul critère affectent également le classement moyen pondéré si les critères sont utilisés dans la moyenne pondérée.
Dans le tri hiérarchique, spécifiez les tolérances par rapport au score du critère et non par rapport à la statistique de validation croisée. Pour les critères dont le score est égal à la statistique (précision de prévision la plus élevée, pire erreur la plus faible et précision la plus élevée), les valeurs de tolérance appropriées sont généralement claires. Par exemple, si la valeur d’erreur quadratique moyenne la plus faible des résultats d'interpolation est 200, une tolérance de 10 % inclut tous les résultats dont les valeurs d'erreur quadratique moyenne sont inférieures ou égales à 220 : 200 + (10/100) x 200 = 220. De même, une tolérance absolue de 15 inclut tous les résultats dont les valeurs d'erreur quadratique moyenne sont inférieures ou égales à 215 : 200 + 15 = 215.
Toutefois, pour les critères dont le score n'est pas égal à la valeur de la statistique (bias le plus faible et précision d'erreur type la plus élevée), les valeurs de tolérance appropriées sont moins claires. Pour la statistique d'erreur moyenne, le bias est évalué en fonction de la valeur absolue de l'erreur moyenne. Cela signifie, par exemple, que les valeurs d'erreur moyenne -4 et 6 possèdent un écart absolu de 50 % car leur différence en valeur absolue est de 50 % : ABS(-4) + (50/100) x ABS(-4) = ABS(6). De même, leur écart absolu est de 2 : ABS(-4) + 2 = ABS(6).
Pour la statistique d'erreur quadratique moyenne standardisée, la précision de l'erreur standard est évaluée en fonction de l'écart absolu entre la valeur de l'erreur quadratique moyenne standardisée et la valeur idéale 1. Cela signifie, par exemple, que les valeurs d'erreur quadratique moyenne standardisée 0,2 et 2,4 possèdent un écart absolu de 75 %. Pour en comprendre la raison, lorsque nous comparons les valeurs 0,2 et 2,4, cette dernière est 1,75 fois plus éloignée (augmentation de 75 %) de la valeur idéale 1 que la première (écarts absolus de 0,8 et 1,4, respectivement) : ABS(0.2 - 1) + (75/100) x ABS(0.2 - 1) = ABS(2.4 - 1). De même, leur écart absolu est de 0,6 : ABS(0.2 - 1) + 0.6 = ABS(2.4 - 1).
Différents critères exigent que tous les résultats d’interpolation prennent en charge le type de sortie d’erreur standard. Par défaut, les options du paramètre Méthodes d’interpolation admettent toutes les options de tous les paramètres. Toutefois, si l’option Pondération par l’inverse de la distance, Fonctions de base radiale ou Interpolation polynomiale globale est spécifiée, différentes options de plusieurs paramètres ne sont plus disponibles, car ces méthodes ne peuvent pas calculer les erreurs standard de prévision. Les options indisponibles sont relatives à la précision d’erreur standard, à la précision, à la statistique d’erreur quadratique moyenne standardisée ou à la statistique d’erreur standard moyenne.
L'option Réduction d'erreur minimum en pourcentage du paramètre Critères d'exclusion est particulièrement utile si vous ne connaissez pas les valeurs ou la plage des points interpolés (par exemple, dans un environnement automatisé). Cette option exclut les résultats d'interpolation qui ne sont pas suffisamment plus précis qu'un modèle de référence non spatial qui prévoit la valeur moyenne globale à toutes les localisations sur la carte. Cette précision relative est mesurée en comparant la valeur de l'erreur quadratique moyenne à l'écart type des valeurs des points interpolés et l'erreur quadratique moyenne doit être au moins inférieure du pourcentage spécifié à l'écart type à inclure dans la comparaison. Par exemple, la valeur 10 signifie que l'erreur quadratique moyenne doit être au moins de 10 % inférieure à l'écart type à inclure dans la comparaison et le classement.
Les différentes disciplines possèdent des normes différentes en matière de réductions d'erreur acceptables dans les résultats d'interpolation. En sciences physiques, où les échantillons de mesures sont plus denses, les erreurs sont souvent réduites de plus de 90 %. En sciences sociales, cependant, des réductions d'erreur de seulement 10 à 20 % sont souvent importantes pour les chercheurs.
Chaque option de paramètre Méthodes d’interpolation génère entre 1 et 5 résultats d’interpolation. Par défaut, 11 résultats sont générés. Si toutes les options sont choisies, 20 résultats sont générés. La table suivante présente les 20 valeurs possibles du champ Description de la valeur Table de validation croisée en sortie avec des détails sur le résultat. Pour approfondir l’examen des résultats, la troisième colonne donne une procédure de création d’une couche géostatistique du résultat à l’aide de l’Assistant géostatistique.
Remarque :
Dans les instructions de création du résultat d’interpolation, il est pris pour hypothèse que vous avez ouvert l’Geostatistical Wizard, choisi la méthode d’interpolation dans la fenêtre de gauche et indiqué les points et le champ dans la fenêtre de droite. Pour un krigeage simple, ordinaire et universel, le type de krigeage est spécifié sur la deuxième page de l’assistant. Sur la première page, utilisez Krigeage/cokrigeage pour les trois types. Si les instructions commencent sur une page particulière de l’assistant, cliquez sur Suivant pour accéder à cette page sans modifier les paramètres. À la fin des instructions, cliquez sur Terminer, puis sur OK pour ajouter le résultat d’interpolation à la carte.
Valeur de champ Description Création Krigeage simple - Par défaut
Modèle de krigeage simple avec les paramètres par défaut. Par défaut, le krigeage simple utilise une transformation.
Aucune modification n’est nécessaire.
Krigeage simple - Optimisé
Modèle de krigeage simple avec des paramètres optimisés.
Sur la page de semi-variogramme (page 4), cliquez sur le bouton Optimiser le modèle
 .
.Krigeage simple - Tendances
Modèle de krigeage simple avec suppression des tendances et aucune transformation.
Sur la deuxième page, définissez Type de transformation sur Aucun et Ordre de suppression des tendances sur Premier.
Krigeage simple - Tendances et transformation
Modèle de krigeage simple avec suppression des tendances et une transformation.
Sur la deuxième page, définissez Ordre de suppression des tendances sur Premier.
Krigeage ordinaire - Par défaut
Modèle de krigeage ordinaire avec paramètres par défaut.
Aucune modification n’est nécessaire.
Krigeage ordinaire - Optimisé
Modèle de krigeage ordinaire avec des paramètres optimisés.
Sur la page de semi-variogramme (page 4), cliquez sur le bouton Optimiser le modèle
 .
.Krigeage universel - Par défaut
Modèle de krigeage universel avec premier ordre de suppression des tendances et paramètres par défaut.
Sur la deuxième page, définissez Ordre de suppression des tendances sur Premier.
Krigeage universel - Optimisé
Modèle de krigeage universel avec premier ordre de suppression des tendances et paramètres optimisés.
Sur la deuxième page, définissez Ordre de suppression des tendances sur Premier. Sur la page de semi-variogramme (page 4), cliquez sur le bouton Optimiser le modèle
 .
.Krigeage bayésien empirique - Par défaut
Modèle de Krigeage bayésien empirique avec paramètres par défaut.
Aucune modification n’est nécessaire.
Krigeage bayésien empirique - Avancé
Modèle de krigeage bayésien empirique avancé utilisant de plus grands sous-ensembles, une superposition plus importante et des simulations.
Sur la seconde page, modifiez les paramètres suivants en remplaçant les valeurs indiquées :
- Taille du sous-ensemble — 200
- Facteur de superposition — 300
- Nombre de simulations — 2
- Transformation — Empirique
- Type de semi-variogramme — K de Bessel décomposé
Interpolation (polynomiale locale) par noyaux
Modèle d’interpolation (polynomiale locale) par noyaux avec paramètres par défaut.
Aucune modification n’est nécessaire. Interpolation par noyaux et Interpolation polynomiale locale sont disponibles sur la première page. Ces méthodes utilisent l’interpolation par noyaux, mais étant donné qu’elles sont analogues, vous devez vous attendre à obtenir des résultats similaires de l’interpolation polynomiale locale.
Pondération par l’inverse de la distance - Par défaut
Modèle de pondération par l’inverse de la distance avec valeur de puissance égale à 2 (par défaut).
Aucune modification n’est nécessaire.
Pondération par l’inverse de la distance - Optimisée
Modèle de pondération par l’inverse de la distance avec valeur de puissance optimisée.
Sur la deuxième page, cliquez sur le bouton Optimiser
 qui apparaît en regard du paramètre Puissance.
qui apparaît en regard du paramètre Puissance.Fonctions de base radiale - Spline entièrement régularisée
Modèle de fonctions de base radiale utilisant une fonction de noyau Spline entièrement régularisée.
Aucune modification n’est nécessaire. La spline entièrement régularisée est la fonction de noyau par défaut pour les fonctions de base radiale.
Fonctions de base radiale - Spline avec tension
Modèle de fonctions de base radiale utilisant une fonction de noyau Spline avec tension.
Sur la deuxième page, remplacez le paramètre Fonction de noyau par Spline avec tension.
Fonctions de base radiale - Multiquadratique
Modèle de fonctions de base radiale utilisant une fonction de noyau Multiquadratique.
Sur la deuxième page, remplacez le paramètre Fonction de noyau par Multiquadratique.
Fonctions de base radiale - Multiquadratique inverse
Modèle de fonctions de base radiale utilisant une fonction de noyau Multiquadratique inverse.
Sur la deuxième page, remplacez le paramètre Fonction de noyau par Multiquadratique inverse.
Fonctions de base radiale - Spline de plaque mince
Modèle de fonctions de base radiale utilisant une fonction de noyau Spline de plaque mince.
Sur la deuxième page, remplacez le paramètre Fonction de noyau par Spline de plaque mince.
Interpolation polynomiale globale - Second ordre
Modèle d’interpolation polynomiale globale avec tendance (quadratique) de second ordre.
Sur la seconde page, attribuez la valeur 2 au paramètre Ordre du polynôme.
Interpolation polynomiale globale - Troisième ordre
Modèle d’interpolation polynomiale globale avec tendance (cubique) de troisième ordre.
Sur la seconde page, attribuez la valeur 3 au paramètre Ordre du polynôme.
Paramètres
arcpy.ga.ExploratoryInterpolation(in_features, value_field, out_cv_table, {out_geostat_layer}, {interp_methods}, {comparison_method}, {criterion}, {criteria_hierarchy}, {weighted_criteria}, {exclusion_criteria})| Nom | Explication | Type de données |
in_features | Points en entrée représentant les emplacements des points à interpoler. | Feature Layer |
value_field | Champ contenant les valeurs à interpoler. | Field |
out_cv_table | Table en sortie contenant les statistiques de validation croisée et les classements de chaque résultat d'interpolation. Les classements finaux des résultats d'interpolation sont stockés dans le champ RANK. | Table |
out_geostat_layer (Facultatif) | Couche géostatistique en sortie du résultat d'interpolation de classement le plus élevé. Ce résultat d'interpolation possède la valeur 1 dans le champ RANK de la table de validation croisée en sortie. En cas d'égalités pour le résultat d'interpolation de classement le plus élevé ou si tous les résultats sont exclus par les critères d'exclusion, la couche n'est pas créée, même si une valeur est fournie. Des messages d'avertissement sont renvoyés par l'outil si cela se produit. | Geostatistical Layer |
interp_methods [interp_methods,...] (Facultatif) | Spécifie les méthodes d’interpolation qui seront utilisées sur les entités en entrée et un champ de valeur. Pour chaque méthode spécifiée, 1 à 5 résultats d’interpolation sont générés. Par défaut, toutes les méthodes sont générées, à l’exception de la pondération par l’inverse de la distance, des fonctions de base radiale et de l’interpolation polynomiale globale (ces méthodes ne pouvant pas créer d’erreurs standard de prévision). Par défaut, 11 résultats d’interpolation sont générés. Si toutes les options sont spécifiées, 20 résultats d’interpolation sont générés.
| String |
comparison_method (Facultatif) | Spécifie la méthode à utiliser pour comparer et classer les résultats d'interpolation.
| String |
criterion (Facultatif) | Spécifie le critère à utiliser pour classer les résultats d'interpolation.
| String |
criteria_hierarchy [[criteria1, tol_type1, tol_val1], [criteria2, tol_type2, tol_val2],...] (Facultatif) | Hiérarchie des critères utilisée pour le tri hiérarchique avec tolérances. Spécifiez plusieurs critères suivant leur ordre de priorité, le premier étant le plus important. Les résultats d'interpolation sont classés en fonction du premier critère et les égalités sont départagées en fonction du deuxième critère. Les égalités dans le deuxième critère sont départagées en fonction du troisième critère et ainsi de suite. Les statistiques de validation croisée étant des valeurs continues qui ne contiennent généralement pas d'égalités exactes, des tolérances sont utilisées pour induire des égalités dans les critères. Pour chaque ligne, spécifiez un critère dans la première colonne, un type de tolérance (en pourcentage ou valeur absolue) dans la deuxième colonne et une valeur de tolérance dans la troisième colonne. Si aucune valeur de tolérance n'est fournie, aucune tolérance n'est utilisée ; cela est particulièrement utile pour la dernière ligne afin d'éviter les égalités pour le résultat d'interpolation de classement le plus élevé. Pour chaque ligne (niveau de la hiérarchie), les critères suivants sont disponibles :
Par exemple, vous pouvez spécifier une valeur ACCURACY avec une tolérance de 5 % sur la première ligne et une valeur BIAS sans tolérance sur la deuxième ligne. Ces options classent d'abord les résultats d'interpolation en fonction de l'erreur quadratique moyenne la plus faible (précision de prévision la plus élevée) et tous les résultats d'interpolation dont les valeurs d'erreur quadratique moyenne diffèrent de moins de 5 % du résultat le plus précis sont considérés comme égaux par la précision de prévision. Parmi les résultats égaux, celui qui possède l'erreur moyenne la plus proche de zéro (bias le plus faible) reçoit le classement le plus élevé. | Value Table |
weighted_criteria [[criteria1, weight1], [criteria2, weight2],...] (Facultatif) | Plusieurs critères avec pondérations à utiliser pour classer les résultats d'interpolation. Pour chaque ligne, spécifiez un critère et une pondération. Les résultats d'interpolation sont classés indépendamment en fonction de chacun des critères et une moyenne pondérée des classements est utilisée pour déterminer les classements finaux des résultats d'interpolation.
| Value Table |
exclusion_criteria [[criteria1, value1], [criteria2, value2],...] (Facultatif) | Critères et valeurs associées à utiliser pour exclure de la comparaison des résultats d'interpolation. Les résultats exclus ne sont pas classés et possèdent la valeur No dans le champ Included de la table de validation croisée en sortie.
| Value Table |
Exemple de code
Le script Python ci-dessous montre comment utiliser la fonction ExploratoryInterpolation.
# Interpolate points using Simple Kriging, Universal Kriging, and EBK
# Rank results by highest prediction accuracy
# Exclude results with error reductions under 25%
inPoints = "myPoints"
inField = "myField"
outTable = "outCVtable"
outGALayer = "Result With Highest Rank"
interpMethods = ["SIMPLE_KRIGING", "UNIVERSAL_KRIGING", "EBK"]
compMethod = "SINGLE"
criterion = "ACCURACY"
exclCrit = [["MIN_PERC_ERROR", 25]]
arcpy.ga.ExploratoryInterpolation(inPoints, inField, outTable, outGALayer,
interpMethods, compMethod, criterion, None, None, exclCrit)Le script Python ci-dessous montre comment utiliser la fonction ExploratoryInterpolation.
# Interpolate points and a field using various interpolation methods
# Rank results by highest weighted average rank
# Rank same results by hierarchical sorting
# Import system modules
import arcpy
# Check out the ArcGIS Geostatistical Analyst extension license
arcpy.CheckOutExtension("GeoStats")
# Allow overwriting output
arcpy.env.overwriteOutput = True
### Set shared parameters
# Set input and output locations
directory = "C:/data/"
ingdb = directory + "data.gdb/"
outgdb = directory + "out.gdb/"
arcpy.env.workspace = directory
# Input points
inPoints = ingdb + "myPoints"
# Input field
inField = "myField"
# List of interpolation methods
interpMethods = ["SIMPLE_KRIGING", "UNIVERSAL_KRIGING", "EBK"]
# Exclude results with error reductions under 25%
exclCrit = [["MIN_PERC_ERROR", 25]]
# Output geostatistical layer with highest rank
outGALayer = "Result With Highest Rank"
### Set weighted average rank parameters
# Output table of ranks and cross validation results
outTable = directory + "outWeightedAverageTable"
# Use weighted average rank
compMethod = "AVERAGE_RANK"
# Use all criteria with highest weight to prediction accuracy
weightedCrit = [
["ACCURACY", 3],
["BIAS", 1],
["WORST_CASE", 1],
["STANDARD_ERROR", 1],
["PRECISION", 1]
]
# Compare using weighted average rank
arcpy.ga.ExploratoryInterpolation(inPoints, inField, outTable, outGALayer,
interpMethods, compMethod, None, None, weightedCrit, exclCrit)
### Set hierarchical sorting parameters
# Output table of ranks and cross validation results
outTable = directory + "outHierSortTable"
# Use hierarchical sorting with tolerances
compMethod = "SORTING"
# Compare using highest prediction accuracy with a 10% tolerance
# Break ties by lowest bias
hierCrit = [
["ACCURACY", "PERCENT", 10],
["BIAS", "PERCENT", None]
]
# Compare using hierarchical sorting with tolerances
arcpy.ga.ExploratoryInterpolation(inPoints, inField, outTable, outGALayer,
interpMethods, compMethod, None, hierCrit, None, exclCrit)Environnements
Informations de licence
- Basic: Nécessite Geostatistical Analyst
- Standard: Nécessite Geostatistical Analyst
- Advanced: Nécessite Geostatistical Analyst
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?