Adapter un modèle au semi-variogramme empirique

Disponible avec une licence Geostatistical Analyst.

La modélisation de la covariance/du semi-variogramme est une étape clé située entre la description spatiale et la prévision spatiale. L’application principale des géostatistiques est la prévision des valeurs de données aux localisations non échantillonnées.

La covariance/le semi-variogramme empirique donne des informations sur l’auto-corrélation spatiale de jeux de données. Toutefois, ils n’indiquent pas toutes les directions et distances possibles. Pour cette raison, et pour s’assurer que les prévisions de krigeage présentent des variances de krigeage positives, il est nécessaire d’ajuster un modèle (c’est-à-dire, une fonction ou courbe continue) à la covariance/au semi-variogramme empirique.

En savoir plus sur la relation entre les semi-variogrammes et la covariance

Différentes vues des valeurs de la covariance/du semi-variogramme empirique

L’assistant géostatistique fournit trois vues différentes des valeurs du semi-variogramme empirique. Vous pouvez utiliser une, deux ou les trois vues pour faciliter l’ajustement d’un modèle aux données. La vue par défaut montre des valeurs de covariance/de semi-variogramme empirique groupées et moyennées. Les contrôles des options de visualisations décrites ci-dessous sont accessibles via le bouton d’options (les trois points verticaux en haut à droite des figures).

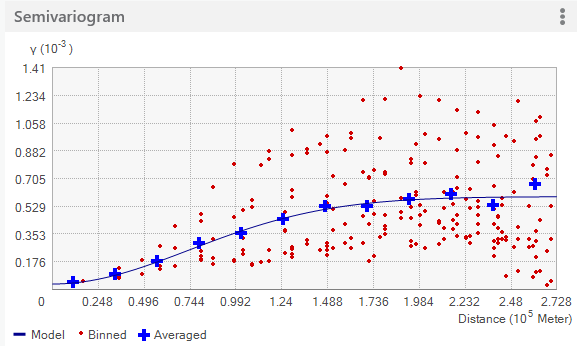
Les valeurs groupées apparaissent sous forme de points rouges et sont générées en groupant les points de covariance/de semi-variogramme empirique à l’aide des cellules carrées dont la largeur est égale à une classe de distance. Les points moyens sont affichés sous forme de croix bleues et sont générés en groupant les points de covariance/de semi-variogramme empirique se trouvant dans les secteurs angulaires. Les points groupés montrent la variation locale dans les valeurs de covariance/semi-variogramme, tandis que les valeurs moyennes montrent la variation lisse dans les valeurs de covariance/semi-variogramme. Il est souvent plus facile d’ajuster un modèle à des valeurs agrégées, car elles offrent une vue moins encombrée de l’auto-corrélation spatiale dans les données et affichent des changements plus lisses dans les valeurs du semo-variogramme que les points groupés.

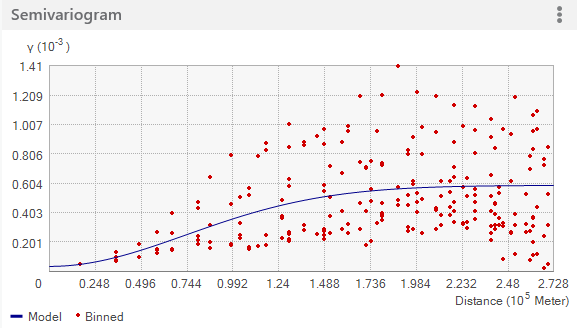
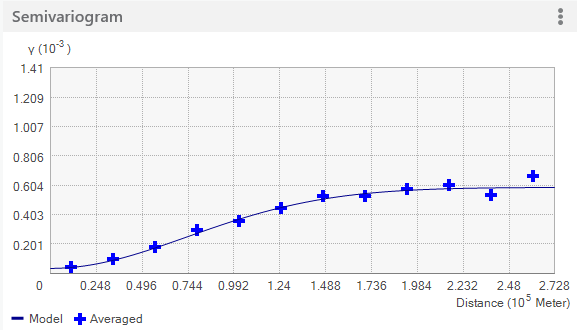
Les deux figures suivantes illustrent uniquement les points groupés (en haut) et uniquement les points moyennés (en bas) :

De plus, les lignes vertes peuvent être ajoutées au dessin à l’aide de l’option Show all lines (Afficher toutes les lignes). Les lignes sont des polynômes locaux ajustés aux valeurs de covariance/de semi-variogramme empirique groupées. La figure suivante montre un exemple typique de ces lignes.

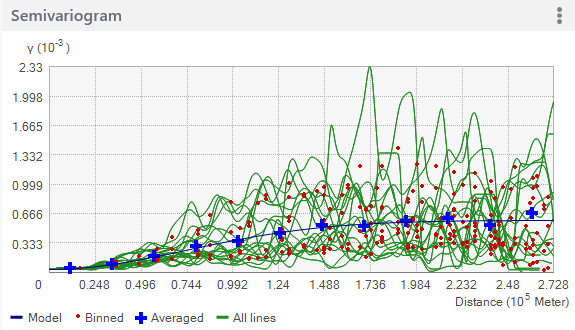
Le modèle de semi-variogramme/covariance que vous ajustez aux données empiriques doit réaliser les opérations suivantes :

• Passer à travers le centre du nuage de valeurs groupées (points rouges).
• Passer aussi près que possible des valeurs moyennées (croix bleues).
• Passer aussi près que possible du milieu des polynômes locaux (lignes vertes).

Gardez à l’esprit que votre connaissance du phénomène peut dicter la forme du modèle, ainsi que ses valeurs de pépite, de portée, de seuil partiel et d’anisotropie, même si le modèle ne semble pas très bien s’ajuster aux données empiriques. Souvenez-vous que les données empiriques ne sont qu’un échantillon du phénomène réel que vous voulez modéliser et qu’elles peuvent ne pas être entièrement représentatives de tous ses aspects spatiaux et statistiques.

Différents types de modèle de covariance/de semi-variogramme

Geostatistical Analyst fournit les fonctions de semi-variogramme/covariance suivantes pour modéliser le semi-variogramme empirique :

• Circulaire
• Sphériques
• Tétrasphérique
• Pentasphérique
• Exponentiel
• Gaussien
• Quadratique rationnel
• À effet de trou
• K de Bessel
• J de Bessel
• Stable

Le modèle sélectionné influence la prévision des valeurs inconnues, plus particulièrement lorsque la forme de la courbe près de l’origine diffère de façon significative. Plus la courbe décline près de l’origine, plus les voisins les plus proches influenceront la prévision.

En conséquence, la surface en sortie sera moins lisse. Chaque modèle est conçu de façon à s'adapter plus précisément à différents types de phénomènes.

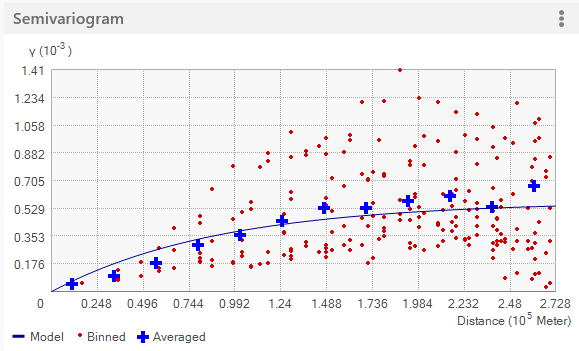
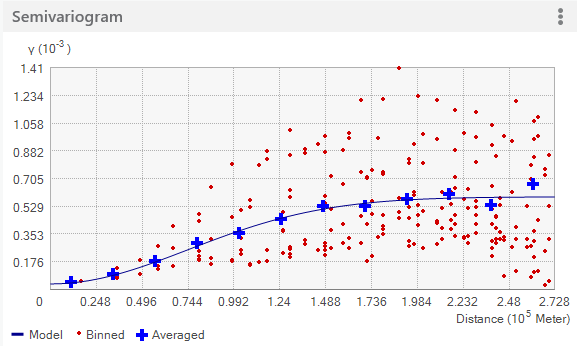
Les diagrammes ci-dessous illustrent deux modèles courants et expliquent la différence entre les deux fonctions. La première figure montre un semi-variogramme exponentiel et le deuxième graphique illustre un semi-variogramme gaussien :