Semi-variogramme et fonctions de covariance

Disponible avec une licence Geostatistical Analyst.

Le semi-variogramme et les fonctions de covariance quantifient le principe selon lequel les objets proches ont tendance à être plus similaires que ceux qui sont éloignés. Le semi-variogramme et la covariance mesurent tous deux la puissance de la corrélation statistique sous forme d’une fonction de la distance.

Le processus de modélisation des semi-variogrammes et des fonctions de covariance consiste à ajuster une courbe de semi-variogramme ou de covariance aux données empiriques. L’objectif consiste à atteindre le meilleur ajustement possible et également d’intégrer votre connaissance du phénomène dans le modèle. Le modèle est ensuite utilisé dans les prévisions.

Lors de l’ajustement d’un modèle, explorez l’auto-corrélation directionnelle dans les données. Le seuil, la plage et la pépite sont des caractéristiques importantes du modèle. Si les données comportent des erreurs de mesure, utilisez un modèle d’erreur de mesure. Suivez ce lien pour apprendre à ajuster un modèle au semi-variogramme empirique.

Semi-variogramme

Le semi-variogramme est défini comme suit

γ(si,sj) = ½ var(Z(si) - Z(sj)),

où var est la variance.

Si deux localisations, s_i et s_j, sont proches l’une de l’autre en termes de mesure de distance d(s_i, s_j), elles sont censées être similaires, donc la différence de leurs valeurs, Z(s_i) - Z(s_j), être petite. Plus la distance entre s_i et s_j augmente, moins elles sont similaires, donc la différence de leurs valeurs, Z(s_i) - Z(s_j), augmente. Vous pouvez le constater dans la figure suivante qui illustre l’anatomie d’un semi-variogramme standard.

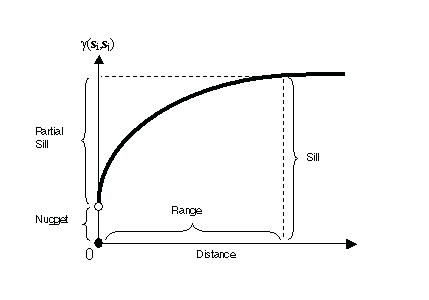
Vous pouvez remarquer que la variance de la différence augmente avec la distance, donc le semi-variogramme peut être considéré comme une fonction de dissemblance. Plusieurs termes sont souvent associés à cette fonction et ils sont également utilisés dans Geostatistical Analyst. La hauteur que le semi-variogramme atteint lorsqu’il se stabilise est appelée seuil. Il est souvent composé de deux parties : une discontinuité à l’origine, appelée effet de pépite, et le seuil partiel ; ces deux éléments ajoutés ensemble constituent le seuil. L’effet de pépite peut lui-même être divisé en une erreur de mesure et une variation spatiale à très petite échelle. L’effet de pépite est simplement la somme de l’erreur de mesure et de la variation à micro-échelle ; puisque l’un ou l’autre de ces composants peut être égal à zéro, l’effet de pépite peut être composé uniquement de l’un ou de l’autre. La distance à laquelle le semi-variogramme se stabilise sur le seuil est appelée plage.

En savoir plus sur les semi-variogrammes, la plage, le seuil et la pépite

Fonction de covariance

La fonction de covariance est définie comme suit

C(si, sj) = cov(Z(si), Z(sj)),

où cov est la covariance.

La covariance est une version à l’échelle de la corrélation. Ainsi, lorsque deux localisations, s_i et s_j, sont proches l’une de l’autre, elles sont censées être similaires et leur covariance (une corrélation) est élevée. Plus la distance entre s_i et s_j augmente, moins elles sont similaires et leur covariance tend vers zéro. Vous pouvez le constater dans la figure suivante qui illustre l’anatomie d’une fonction de covariance standard.

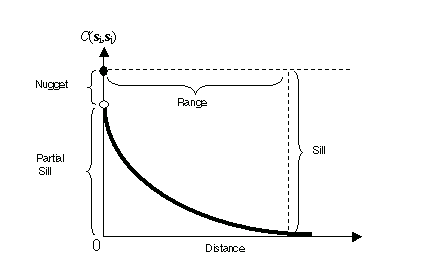
Vous pouvez remarquer que la fonction de covariance diminue avec la distance, donc elle peut être considérée comme une fonction de similarité.

Relations entre le semi-variogramme et la fonction de de covariance

Il existe une relation entre le semi-variogramme et la fonction de covariance :

γ(si, sj) = seuil - C(si, sj),

Cette relation peut être observée dans les figures. Grâce à cette équivalence, vous pouvez réaliser des prévisions dans Geostatistical Analyst avec l’une ou l’autre de ces fonctions. (Tous les semi-variogrammes dans Geostatistical Analyst possèdent des seuils.)

Les semi-variogrammes et les covariances ne peuvent pas être n’importe quelle fonction. Pour que les prévisions aient des erreurs standard de krigeage non négatives, seules certaines fonctions peuvent être utilisées en tant que semi-variogrammes et covariances. Geostatistical Analyst offre plusieurs choix acceptables ; vous pouvez en essayer plusieurs en fonction des données dont vous disposez. Vous pouvez également utiliser des modèles créés par l’ajout de plusieurs modèles ; cette construction fournit des modèles valides ; vous pouvez ajouter jusqu’à quatre d’entre eux dans Geostatistical Analyst. Dans certains cas, il existe des semi-variogrammes, mais pas de fonctions de covariance. Par exemple, dans le cas d’un semi-variogramme linéaire qui ne comporte pas de seuil, il n’existe pas de fonction de covariance correspondante. Seuls les modèles avec des seuils sont utilisés dans Geostatistical Analyst. Il n’existe pas de règles strictes quant au choix du « meilleur » modèle de semi-variogramme. Vous pouvez observer le semi-variogramme empirique ou la fonction de covariance et choisir un modèle qui semble approprié. Vous pouvez également utiliser la validation et la validation croisée pour vous guider.