Comprendre le krigeage de probabilités

Disponible avec une licence Geostatistical Analyst.

Le krigeage de probabilités implique le modèle

I(s) = I(Z(s) > ct) = µ1 + ε1(s) Z(s) = µ2 + ε2(s),

où µ₁ et µ₂ sont des constantes inconnues et I(s) est une variable binaire créée par l’utilisation d’un indicateur de seuil, I(Z(s) > c_t).

Vous remarquerez que vous avez maintenant deux types d’erreurs aléatoires, ε₁(s) et ε₂(s), donc il existe une auto-corrélation pour chacune d’entre elles et une corrélation croisée entre elles. Le krigeage de probabilités tend à fonctionner comme le krigeage d’indicatrices, mais il fait appel au cokrigeage dans un souci d’optimisation.

Par exemple, dans la figure suivante, qui utilise les mêmes données que celles employées pour expliquer les concepts du krigeage ordinaire, universel, simple et d’indicatrices, notez la présence de datums étiquetés Z(u=9), avec une variable indicatrice de I(u) = 0, et Z(s=10), avec une variable indicatrice de I(s) = 1.

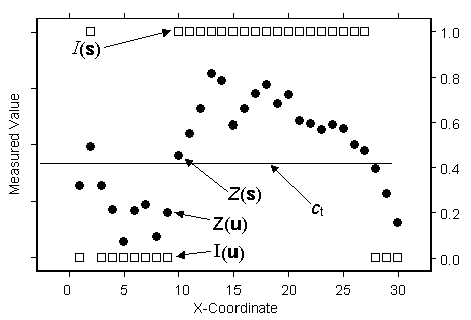
Si vous souhaitez prévoir une valeur à mi-chemin entre les deux, à la coordonnée x de 9,5, l’utilisation du krigeage d’indicatrices seul donnerait une prévision proche de 0,5. Toutefois, vous pouvez constater que Z(s) se situe juste au-dessus du seuil, mais que Z(u) est bien en dessous du seuil. Vous avez donc certaines raisons de penser qu’une prévision d’indicatrices à la localisation 9,5 devrait être inférieure à 0,5. Le krigeage de probabilités tente d’exploiter les informations supplémentaires des données d’origine en plus de la variable binaire. Mais toute cela a un prix. Vous devez procéder à bien plus d’estimations, dont l’estimation de l’auto-corrélation pour chaque variable, ainsi que leur corrélation croisée. À chaque fois que vous estimez des paramètres d’auto-corrélation inconnus, vous introduisez davantage d’incertitude. Le krigeage de probabilités n’en vaut peut-être pas la peine.

Le krigeage de probabilités peut utiliser des semi-variogrammes ou des covariances (formes mathématiques employées pour exprimer l’auto-corrélation), des covariances croisées (formes mathématiques utilisées pour exprimer la corrélation croisée) et des transformations, mais il n’admet pas l’erreur de mesure.