L’outil Corrélation croisée de séries chronologiques permet de comparer deux séries chronologiques (appelées variables d’analyse principale et secondaire) à chaque localisation d’un cube spatio-temporel en calculant un coefficient de corrélation Pearson entre les valeurs correspondantes à chaque intervalle temporel. De plus, la variable d’analyse secondaire est décalée (déplacée) dans le temps par rapport à la variable d’analyse principale et les nouvelles corrélations sont calculées pour les différents décalages. Vous pouvez ainsi estimer n’importe quel effet à retardement entre les variables d’analyse principale et secondaire, comme le décalage entre une campagne de marketing et une augmentation des ventes. Par exemple, si la corrélation entre marketing et ventes est maximale lorsque le chiffre d’affaires est décalé d’une semaine en arrière, cela signifie qu’il existe un décalage d’une semaine entre les augmentations en marketing et les augmentations de chiffres d’affaires.
L’outil peut être utilisé comme méthode d’exploration et de description pour calculer la corrélation brute entre les séries chronologiques. Vous pouvez aussi l’utiliser comme méthode explicative et inférentielle en retirant les tendances et en faisant un filtre sur l’auto-corrélation afin d’isoler la dépendance statistique entre les deux variables. Vous pouvez également inclure des voisins dans les calculs pour incorporer les similarités entre les séries chronologiques de localisations voisines et capturer les interactions et les effets spatiaux.
Applications possibles
Voici quelques exemples d’application de l’outil :
- Dans une zone métropolitaine, comparez les températures par heure à la consommation électrique afin d’anticiper les pics de demande pendant les heures les plus chaudes de chaque jour.
- Estimez le décalage entre l’augmentation du niveau des précipitations et l’augmentation du volume d’eau dans les réservoirs. Combien de temps après le pic d’un orage le niveau d’eau dans les réservoirs augmente-t-il le plus rapidement ? Ce délai varie-t-il dans les localisations où les conditions du sol sont différentes ?
- Comparez l’efficacité de différentes campagnes marketing pour déterminer celle dont les dépenses sont les mieux corrélées de façon positive au chiffre d’affaires. Vous pouvez également estimer le délai entre dépenses de marketing et achats des clients. Est-ce que certaines campagnes prennent plus de temps pour engendrer des ventes, mais finissent par s’avérer plus efficaces à générer un revenu à long terme ?
Corrélation croisée
Les valeurs de corrélation croisée mesurent la force de la relation linéaire entre deux séries chronologiques : lorsque l’une d’elles augmente, est-ce que l’autre a tendance à augmenter, diminuer ou rester stable ? Si la valeur de la corrélation croisée est proche de 1, cela signifie que les deux séries chronologiques évoluent dans la même direction et dans les mêmes proportions. Par exemple, le nombre de passagers et le prix des billets d’une compagnie aérienne sont fortement corrélés de façon positive : plus de passagers voyagent, plus les prix des billets augmentent. De même, une corrélation croisée négative signifie que deux séries chronologiques évoluent dans des directions opposées. Par exemple, le nombre de places de parking libres et le niveau de circulation dans les rues (la circulation augmente s’il y a moins de places pour stationner). Si les deux séries chronologiques ne sont pas liées et n’ont pas tendance à évoluer dans le même sens ou dans des directions opposées, la corrélation croisée est proche de zéro.
Décalages temporels
Comme on note souvent des effets à retardement entre deux séries chronologiques (par exemple, le délai entre l’augmentation du nombre de prédateurs dans un écosystème et la diminution de la population des proies), les valeurs de corrélation croisée sont toujours calculées par rapport à un décalage temporel. Le décalage temporel consiste à déplacer la variable secondaire par rapport à la variable principale. Une nouvelle valeur de corrélation croisée est calculée pour les nouvelles paires correspondantes de valeurs entre les deux séries chronologiques.
Dans l’image ci-dessous, le diagramme du haut montre les variables d’analyse principale et secondaire. Le diagramme du milieu illustre la variable secondaire déplacée vers le futur de deux intervalles temporels (décalage temporel 2), et celui du bas la variable secondaire déplacée dans le passé de deux intervalles temporels (décalage temporel -2). Comme il apparaît que la variable secondaire augmente ou diminue en même temps que la variable principale; le fait de la déplacer dans le passé (décalages temporels négatifs) augmente la corrélation croisée entre les variables. Remarquez en outre que certains des intervalles temporels aux extrémités des séries chronologiques de la variable principale n’ont plus de valeurs appariées dans la variable secondaire après le décalage.
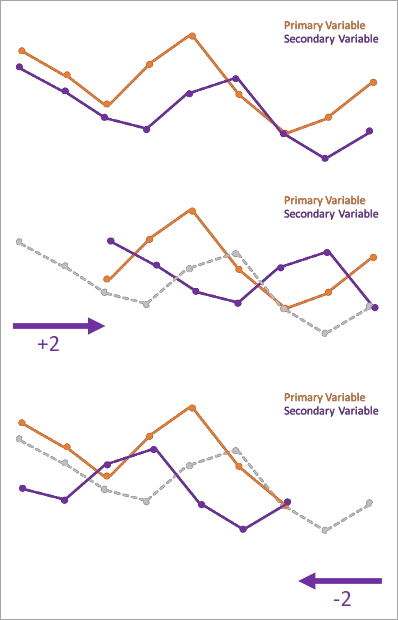
Si le décalage temporel qui présente la corrélation la plus forte est positif, les variations de la valeur de la variable d’analyse secondaire se produisent avant celles de la variable d’analyse principale. De même, si le décalage temporel qui présente la corrélation la plus forte est négatif, les variations de la variable d’analyse principale se produisent avant celles de la variable d’analyse secondaire.
L’outil calcule les corrélations croisées pour tous les décalages temporels entre zéro et la valeur du paramètre Décalage temporel maximal. En outre, le paramètre Direction du décalage pour la variable secondaire peut permettre de spécifier la direction du déplacement (autrement dit, le signe du décalage temporel). Vous pouvez déplacer la variable d’analyse secondaire dans les deux directions, dans le passé (décalage temporel négatif) ou vers le futur (décalage temporel positif). Par exemple, avec un décalage temporel maximal de 10 et un déplacement dans les deux directions, les corrélations croisées sont calculées pour tous les décalages temporels entre -10 et 10. De même, avec un décalage temporel maximal de 5 et un déplacement uniquement vers le futur, les corrélations croisées sont calculées pour tous les décalages temporels entre -5 et 0.
Remarque :
Si aucune valeur n’est indiquée pour le paramètre Décalage temporel maximal, celui-ci est de 10*log10(T/2), pour T intervalles temporels dans chaque série chronologique (arrondi à la baisse). La valeur ne peut pas être supérieure à (T-5). Si vous indiquez la valeur zéro, seule la corrélation brute des deux séries chronologiques, sans aucun décalage temporel, est calculée.
Inclure les voisins spatiaux
Le paramètre Inclure des voisins spatiaux dans les calculs vous permet de définir un voisin autour de chaque localisation afin d’améliorer l’estimation de la corrélation croisée. Si les voisins sont inclus, la corrélation croisée de chaque localisation pour un décalage temporel donné est la moyenne (éventuellement pondérée) des corrélations croisées entre la variable d’analyse principale de la localisation focale et la variable d’analyse secondaire décalée temporellement de chaque voisin spatial (et elle-même).
Dans l’image ci-dessous, par exemple, la localisation focale est illustrée en rouge et entourée de huit voisins. La série chronologique en orange est la variable d’analyse principale de la localisation focale, tandis que les séries chronologiques en violet correspondent aux variables d’analyse secondaires à la localisation focale et à chaque voisin. Dans ce cas, la corrélation croisée à la localisation focale est la moyenne de neuf corrélations croisées : la corrélation croisée de l’entité focale avec elle-même, celle de la localisation focale avec le premier voisin, celle de la localisation focale avec le deuxième voisin, et ainsi de suite. Dans chaque comparaison, la variable d’analyse principale de la localisation focale est comparée à la variable secondaire du voisin (ou elle-même). En faisant la moyenne des corrélations, la valeur caractérise mieux la corrélation croisée de la surface plutôt que de la localisation individuelle. Ce calcul de la moyenne est répété pour tous les décalages temporels et toutes les localisations.
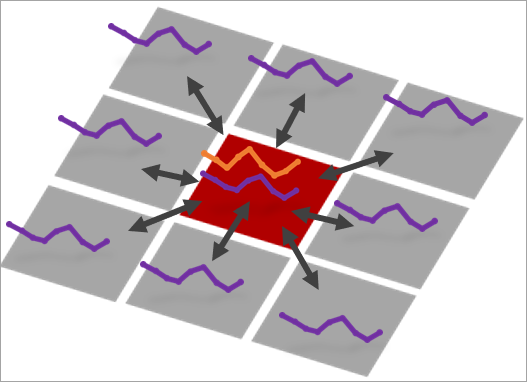
Par défaut, chaque corrélation est pondérée de façon égale dans la moyenne. Mais si vous utilisez un canal de distance ou un voisinage de k voisins les plus proches, le paramètre Méthode de pondération des voisins spatiaux vous permet de donner des pondérations plus importantes aux voisins les plus proches de la localisation focale. Vous pouvez utiliser un noyau bicarré ou gaussien pour définir les pondérations.
Remarque :
Pour les voisinages de canal de distance, la bande passante de chaque noyau est égale au canal de distance. Pour plus d’informations sur le mode de calcul de la bande passante par défaut, reportez-vous à la rubrique Fonctionnement de l’outil Densité de noyau. Pour les voisinages de k voisins les plus proches, la bande passante est égale à la distance du (k+1)e voisin. Cela garantit que tous les k voisins sont plus proches que la bande passante et ont des pondérations non nulles. Pour les localisations de polygone, les distances de centroïde à centroïde servent à déterminer les voisins et les pondérations.
Filtrer et supprimer les tendances
Pour un décalage temporel donné, la corrélation croisée entre deux séries chronologiques mesure si celles-ci ont tendance à augmenter ou diminuer ensemble. Cela peut être considéré comme une analyse descriptive qui expose et estime la mesure dans laquelle les valeurs correspondent. Toutefois, la corrélation croisée brute se compose de différents facteurs, notamment les tendances, la saisonnalité, l’auto-corrélation et la dépendance statistique des variables. Les valeurs brutes de deux séries chronologiques peuvent être fortement corrélées simplement du fait de l’auto-corrélation et de tendances communes. Par exemple, les ventes de crème solaire et de glaces sont fortement corrélées, mais si vous supprimez les tendances économiques et saisonnières, la corrélation devient très faible. Vous pouvez supprimer les tendances, la saisonnalité et l’auto-corrélation (souvent appelés préblanchiment et filtrage) en activant le paramètre Filtrer et supprimer les tendances.
Il est important de filtrer et supprimer les tendances, particulièrement lorsque l’objectif est d’estimer le décalage temporel optimal entre les variables. Par exemple, dans des données épidémiologiques, il existe un décalage temporel entre l’augmentation du nombre de maladies et l’augmentation des hospitalisations. Toutefois, si on utilise les valeurs brutes de ces nombres, on constate fréquemment l’absence de décalage temporel entre maladie et hospitalisation du fait de l’auto-corrélation et des tendances fortes (en d’autres termes, le décalage temporel zéro présente la corrélation la plus forte). En revanche, en supprimant les tendances et en filtrant l’auto-corrélation, le véritable décalage temporel entre maladie et hospitalisation (10 jours, par exemple) affiche souvent la corrélation la plus forte.
Étant donné que les tendances, la saisonnalité et l’auto-corrélation contribuent toutes à gonfler le taux d’erreur de type-1 des tests statistiques, les valeurs p et les intervalles de confiance de 95 pour cent des corrélations croisées ne sont calculés que si vous filtrez et supprimez les tendances des deux séries chronologiques. De plus, les valeurs p et les intervalles de confiance ne peuvent être calculés que pour des comparaisons par paires de deux séries chronologiques. En d’autres termes, si vous incluez les voisins spatiaux dans les calculs, les valeurs p et les intervalles de confiance ne sont pas calculés pour la moyenne pondérée des corrélations croisées. Vous pouvez cependant utiliser le paramètre Table des corrélations deux par deux en sortie pour créer une table contenant des valeurs p et des intervalles de confiance entre chaque localisation et chaque voisin à tous les décalages temporels.
Remarque :
Les valeurs p et les intervalles de confiance sont calculés en faisant l’hypothèse d’une distribution normale des corrélations croisées avec un écart type égal à la racine carrée du nombre de décalages temporels. Ce résultat asymptomatique est particulièrement précis pour les séries chronologiques comportant au moins 30 intervalles. Pour les séries chronologiques plus courtes, un avertissement est émis.
Les tests de signification statistique sont réalisés de manière indépendante pour chaque décalage temporel de chaque emplacement, et aucune correction ne se produit pour les tests d’hypothèses multiples. Faites preuve de prudence lorsqu’il s’agit d’interpréter la signification d’une valeur p ou d’un intervalle de confiance en particulier. Toutes les valeurs p sont calculées au moyen de tests bilatéraux d’hypothèses.
Pour plus d’informations sur la façon dont le filtrage et la suppression des tendances sont effectués, reportez-vous à la rubrique Ajuster un modèle de filtrage et de suppression des tendances ci-après.
Sorties de l’outil
La sortie principale de l’outil est une classe d’entités contenant les champs des résultats de corrélation croisée. Dans une carte, la classe d’entités est ajoutée sous forme de groupe de couches contenant six couches, chacune visualisant un champ différent des entités en sortie. Chaque couche comprend une option permettant de naviguer rapidement entre les couches, sans devoir les activer et les désactiver individuellement.
Trois couches affichent des cartes des corrélations les plus fortes : corrélation positive la plus forte, corrélation négative la plus forte et corrélation absolue la plus forte. Chaque localisation est colorée par la corrélation positive la plus importante, la corrélation négative la plus importante et la corrélation la plus importante en valeur absolue.
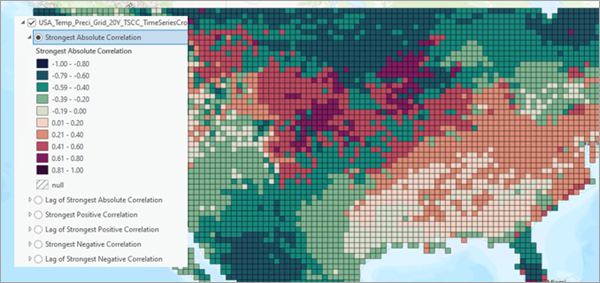
Les trois autres couches affichent les décalages temporels associés aux trois couches des corrélations les plus fortes. Par exemple, le décalage de la couche Corrélation absolue la plus forte affiche le décalage qui résulte des corrélations absolues les plus fortes.
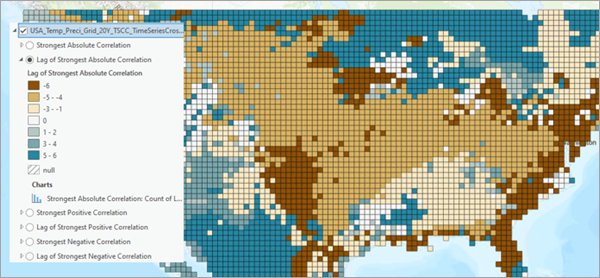
En utilisant ces six couches en même temps, vous pouvez explorer la façon dont la variable d’analyse principale est fortement corrélée à la variable d’analyse secondaire à chaque localisation, et déterminer les décalages temporels qui ont découlé de ces corrélations. Il se peut que des modèles spatiaux figurent dans ces résultats. Par exemple, certaines régions peuvent avoir des décalages temporels moins importants ou des corrélations plus fortes que d’autres. Il se peut aussi qu’une même localisation présente à la fois une corrélation croisée fortement positive et fortement négative selon le décalage temporel. Par exemple, deux séries chronologiques d’une relation cyclique prédateur-proie peuvent être corrélées de façon positive ou négative en déplaçant les cycles des deux séries chronologiques à l’intérieur ou à l’extérieur d’un alignement.
En plus des six champs utilisés dans le groupe de couches, les entités en sortie comportent les champs suivants :
- Champs d’objet et d’ID de localisation.
- Champs de corrélation croisée pour chaque décalage temporel. Un champ distinct est créé pour chaque décalage temporel.
- Nombre de voisins de la localisation. Ce champ n’est créé que si vous incluez des voisins spatiaux dans les calculs.
Si vous filtrez et supprimez les tendances, et n’incluez pas de voisins spatiaux dans les calculs, les champs suivants sont créés pour chacune des corrélations les plus fortes (positive, négative et absolue) :
- Un champ de valeur p qui teste la signification statistique de la corrélation croisée.
- Les champs des limites inférieure et supérieure d’un intervalle de confiance de 95 pour cent pour la corrélation croisée.
- Un champ binaire (0 ou 1) qui indique si la corrélation croisée est significative statistiquement (valeur du champ 1) ou non (valeur du champ 0) à un niveau de confiance de 95 pour cent.
Remarque :
Si toutes les valeurs de corrélation croisée à une localisation sont positives, le champ de corrélation négative la plus forte et le décalage du champ de corrélation négative la plus forte contiennent une valeur nulle pour cette localisation. De même, toutes les corrélations négatives à une localisation produisent des valeurs nulles dans les champs de corrélation positive la plus forte.
Le cube spatio-temporel en entrée sera mis à jour avec les résultats de l’analyse, et vous pouvez utiliser l’outil Visualiser le cube spatio-temporel en 2D avec l’option de thème d’affichage Résultats de la corrélation croisée de séries chronologiques pour recréer le groupe de couches et la classe d’entités en sortie. La variable d’analyse avec les résultats de corrélation croisée correspondra aux noms des variables d’analyse principale et secondaire avec un tiret de soulignement entre les deux. Par exemple, si les variables en entrée sont nommées MARKETING et SALES, la variable d’analyse avec les résultats est nommée MARKETING_SALES.
Diagrammes contextuels
Vous pouvez créer des diagrammes contextuels interactifs à partir des entités en sortie en activant le paramètre Activer les fenêtres contextuelles de série chronologique. Si ces diagrammes sont créés, l’outil Explorer vous permet de cliquer sur une entité pour afficher un diagramme à barres des corrélations croisées pour chaque décalage temporel, ainsi qu’un diagramme linéaire montrant les variables d’analyse principale et secondaire.
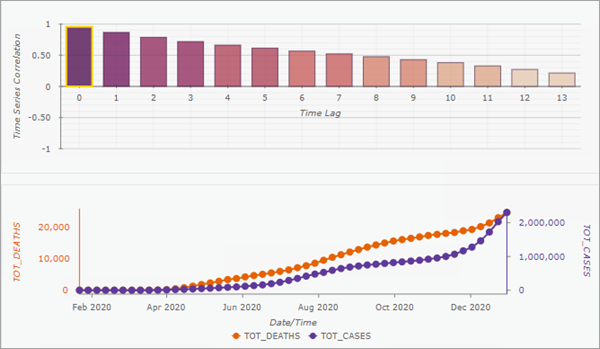
Survolez les barres du diagramme pour que les séries chronologiques correspondantes en dessous se déplacent du décalage temporel associé. Cela permet de voir comment les deux séries chronologiques s’alignent après les différents décalages temporels.
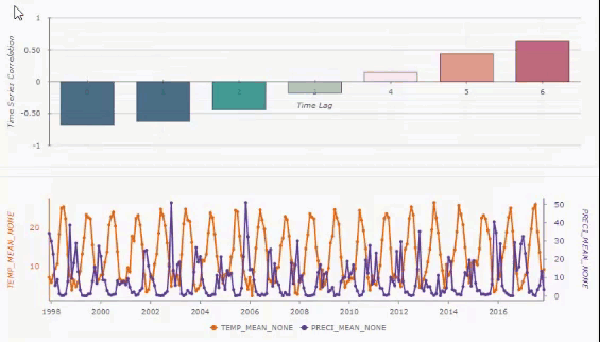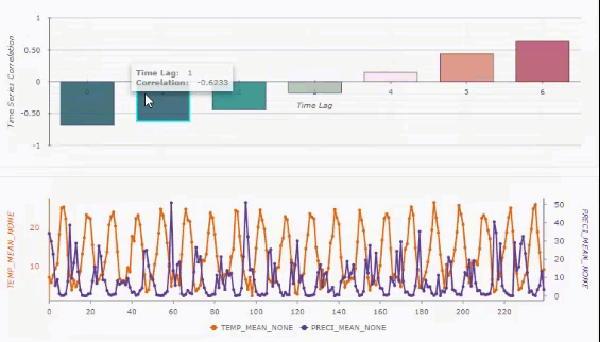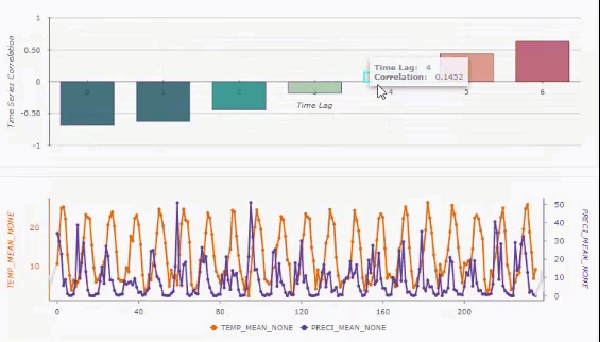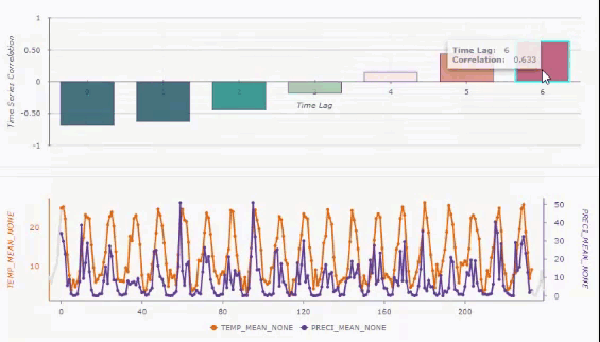
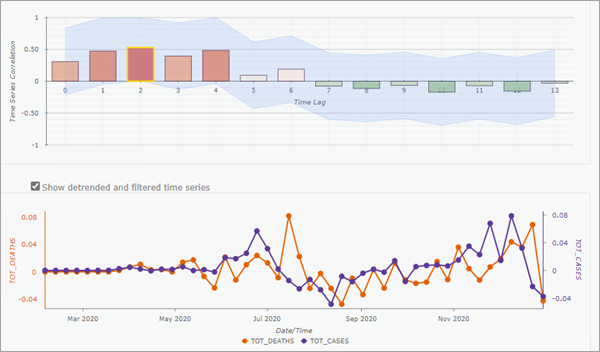
Si vous filtrez et supprimez les tendances, et n’incluez pas de voisins spatiaux, le diagramme contextuel affiche les intervalles de confiance de 95 pour cent (ombrage bleu clair) autour des corrélations croisées de chaque décalage temporel. La case à cocher Afficher les séries chronologiques décomposées et filtrées vous permet d’afficher les valeurs brutes des séries chronologiques ou les séries chronologiques après filtrage et suppression des tendances.
Remarque :
Si vous incluez des voisins spatiaux dans les calculs, seul le diagramme à barres des décalages temporels s’affiche. Cela évite d’afficher trop de séries chronologiques dans chaque diagramme contextuel
Les diagrammes de fenêtre contextuelle ne sont pas créés lorsque les entités en sortie sont enregistrées en tant que shapefile (.shp).
Tables de corrélation en sortie
Si vous le souhaitez, vous pouvez utiliser le paramètre Table des corrélations décalées en sortie pour enregistrer les résultats des corrélations croisées sous forme de table. Dans la table, chaque ligne contient la corrélation pour une seule localisation et un seul décalage temporel. Le nombre de lignes contenues dans la table est ainsi égal au nombre de localisations multiplié par le nombre de décalages temporels. De plus, si vous filtrez et supprimez les tendances, et n’incluez pas de voisins spatiaux, la table contient des champs de la valeur p et les limites supérieure et inférieure d’un intervalle de confiance de 95 pour cent. Enregistrer les informations ligne par ligne sous forme de table (plutôt que sous forme de champs des entités en sortie) est souvent plus pratique pour exporter et analyser les résultats des corrélations croisées. La table peut aussi être jointe à nouveau aux localisations à des fins d’analyses supplémentaires.
Si vous incluez des voisins spatiaux dans les calculs, vous pouvez également utiliser le paramètre Table des corrélations deux par deux en sortie pour créer une table contenant des comparaisons entre chaque localisation focale et chaque voisin pour chaque décalage temporel. Par exemple, s’il y a 10 localisations, 5 décalages temporels et 7 voisins par localisation, la table en sortie comptera 10*5*(7+1)=400 lignes (le nombre 1 est ajouté pour inclure les comparaisons de la localisation focale avec elle-même). Pour chaque combinaison, la corrélation croisée associée est stockée sous forme de champ. Si vous filtrez et supprimez les tendances, la table contient également des champs de la valeur p et les limites supérieure et inférieure d’un intervalle de confiance de 95 pour cent.
Messages de géotraitement
L’outil fournit un certain nombre de messages d’informations sur les résultats de l’outil. Les messages comportent deux sections.
La section Input Space Time Cube Details (Détails du cube spatio-temporel en entrée) affiche les propriétés du cube spatio-temporel en entrée ainsi que des informations sur l’intervalle de pas de temps, le nombre de pas de temps, le nombre d’emplacements et le nombre de groupes spatio-temporels. Les propriétés affichées dans cette première section dépendent de la façon dont le cube a été créé, de sorte que les informations varient d’un cube à l’autre.
La section Résumé des corrélations par décalage temporel affiche un tableau des résumés statistiques des corrélations croisées de toutes les localisations pour chaque décalage temporel. Pour chaque décalage temporel, le tableau affiche le minimum, le maximum, la moyenne, l’écart type et le nombre de corrélations croisées de toutes les localisations. Si vous filtrez et supprimez les tendances, et n’incluez pas de voisins spatiaux, la table contient également un nombre de localisations avec des corrélations croisées significatives statistiquement pour chaque décalage temporel. Ces résumés statistiques vous permettent d’identifier rapidement les décalages temporels individuels qui affichent une forte corrélation dans de nombreuses localisations, révélant peut-être des modèles qui passeraient inaperçus dans l’exploration des résultats des localisations individuelles.
Diagrammes
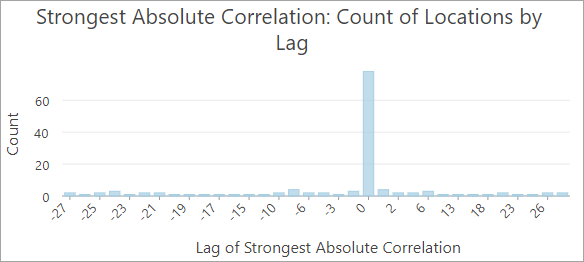
Les trois couches qui affichent les décalages des corrélations les plus fortes (positive, négative et absolue) comprennent chacune un diagramme à barres illustrant les nombres de localisations qui ont la plus forte corrélation pour chaque décalage temporel. Par exemple, dans l’image ci-dessous, la majorité des localisations affichent la corrélation absolue la plus forte avec un décalage temporel de 0, ce qui signifie qu’il n’y a pas de délai estimé entre les deux séries chronologiques à la plupart des localisations.
Formule de la corrélation croisée
Pour un décalage temporel donné, la formule de la corrélation croisée entre deux séries chronologiques est la suivante :
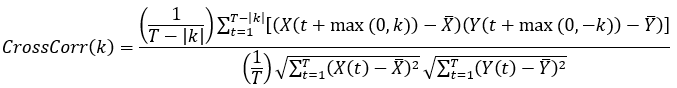
- k est le décalage temporel.
- t est l’intervalle temporel.
- T est le nombre d’intervalles temporels dans chaque série chronologique.
- X(t) est la valeur de la variable d’analyse principale à l’intervalle temporel t.
- Y(t) est la valeur de la variable d’analyse secondaire à l’intervalle temporel t.
- x̄ est la moyenne de la variable d’analyse principale (utilisant tous les intervalles temporels).
- Ȳ est la moyenne de la variable d’analyse secondaire (utilisant tous les intervalles temporels).
Le numérateur et le dénominateur sont divisés par le nombre de termes dans les sommes afin de corriger les biais à l’égard des décalages temporels plus importants.
Ajuster un modèle de filtrage et de suppression des tendances
Si vous filtrez et supprimez les tendances des séries chronologiques, les étapes de prétraitement suivantes sont exécutées sur les variables d’analyse principale et secondaire avant d’effectuer le décalage temporel et de calculer les corrélations croisées :
- Un modèle de régression par la méthode des moindres carrés ordinaires est créé pour prédire la valeur suivante de la variable d’analyse principale à partir de la valeur précédente. Dans le modèle, chaque intervalle temporel sert de variable explicative pour prédire la valeur de l’intervalle temporel suivant.
- Un deuxième modèle des moindres carrés ordinaires est créé pour prédire la valeur suivante de la variable d’analyse principale à partir des deux valeurs précédentes. Par exemple, les deux premiers intervalles temporels sont utilisés pour prédire le troisième ; le deuxième et le troisième sont utilisés pour prédire le quatrième, et ainsi de suite.
- Trois autres modèles des moindres carrés ordinaires sont créés à partir des trois, quatre et cinq valeurs précédentes, respectivement, pour prédire la valeur suivante de la variable d’analyse principale.
- Une transformation de Fourier rapide (FFT, pour Fast Fourier Transform) est utilisée pour estimer la saisonnalité de la variable principale, et un sixième modèle des moindres carrés ordinaires utilise ce nombre d’intervalles temporels pour prédire la valeur suivante.
- Des valeurs AIC sont calculées pour chacun des six modèles des moindres carrés ordinaires et celui dont la valeur est la plus petite est choisi comme modèle de filtrage et de suppression des tendances.
- À l’aide des coefficients du modèle choisi, les résidus sont calculés pour la variable d’analyse principale, et ces résidus deviennent la nouvelle variable principale. Cette étape est souvent appelée préblanchiment de la variable principale, car les résidus sont supposés afficher un bruit blanc aléatoire.
- Les résidus sont calculés pour la variable d’analyse secondaire en appliquant les coefficients aux valeurs de la variable secondaire, et ces résidus deviennent la nouvelle variable secondaire. Cette étape est souvent appelée filtrage de la variable secondaire. Comme les coefficients ont été estimés à partir de la variable principale, les résidus de la variable secondaire sont censés contenir certaines tendances et l’auto-corrélation (plutôt que du bruit blanc aléatoire).
- Ce traitement est répété indépendamment pour chaque localisation. Si les voisins spatiaux sont pris en compte, le traitement est effectué sur la variable principale de la localisation focale et sur la variable secondaire de chaque voisin (et elle-même).
Remarque :
Le traitement de filtrage et de suppression des tendances réduit la longueur de chaque série chronologique du nombre d’intervalles temporels utilisés comme variables explicatives dans le modèle des moindres carrés ordinaires choisi à l’étape 5. Par exemple, si trois intervalles temporels sont utilisés pour prédire la valeur suivante, les résidus ne peuvent pas être calculés pour les trois premiers intervalles temporels de chaque série chronologique.
Bibliographie
Brockwell, P. J., and Davis, R. A. (2002). Introduction to Time Series and Forecasting. New York, NY: Springer New York. https://doi.org/10.1007/978-3-319-29854-2.
Chan, K.S. and Cryer, J.D. (2008). Time Series Analysis With Applications in R. New York, NY: Springer New York. https://doi.org/10.1007/978-0-387-75959-3.
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?
